Calculus
Calculus
本篇微积分内容主要回顾一些重要结论的推导证明,全文没有严格上下文关系。
绘图我是实在肝不动了…索性用个草图好了,将个烂就
催更|辅导|私塾兼职|联系偷偷:LifeGoesOn_Rio
1. 三角函数
三角函数涉及到三角换元,反函数图像,积化和差公式等等..
1.1 三角换元
- 正割:
$$
\sec x = \frac{1}{\cos x}
$$
- 余割:
$$
\csc x = \frac{1}{\sin x}
$$
- 常见换元:
$$
\begin{cases}
\sin^2 x + \cos^2 x = 1 \\
1 + \tan^2 x = \sec^2 = \frac{1}{\cos^2}
\end{cases}
$$
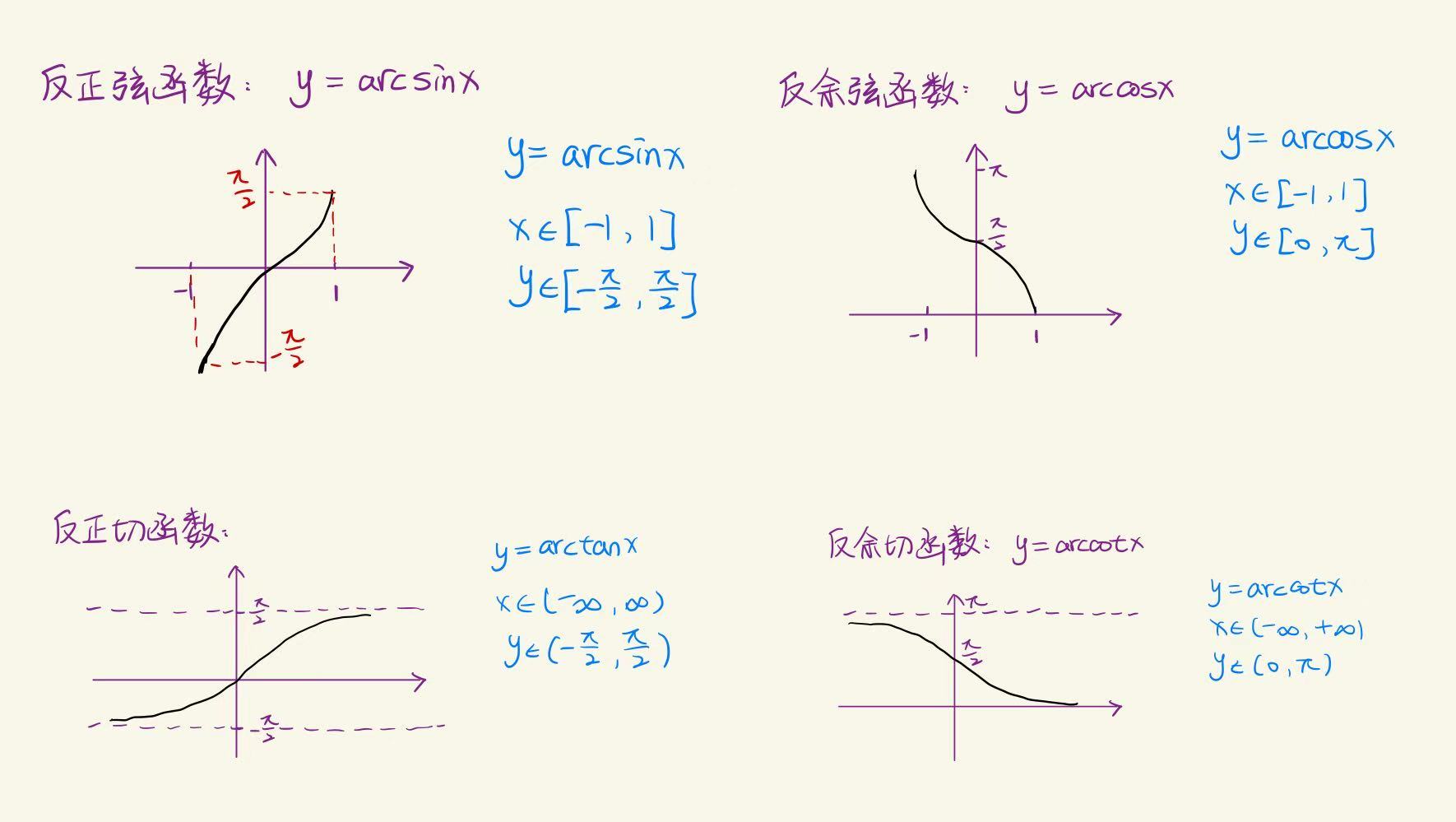
1.2 反三角函数
这里我觉得认识图像非常重要,当然还有后面的反三角函数求导,这里暂不做讲解。
1.2.1 反正弦函数(arcsin(x))
反正弦函数,记作 $\arcsin(x)$,是正弦函数的反函数。它的定义域为 $[-1, 1]$,值域为 $[-\frac{\pi}{2}, \frac{\pi}{2}]$。即对于任意 $y = \arcsin(x)$,有:
$$
\sin(y) = x, \quad y \in \left[-\frac{\pi}{2}, \frac{\pi}{2}\right]
$$
1.2.2 反余弦函数(arccos(x))
反余弦函数,记作 $\arccos(x)$,是余弦函数的反函数。它的定义域为 $[-1, 1]$,值域为 $[0, \pi]$。即对于任意 $y = \arccos(x)$,有:
$$
\cos(y) = x, \quad y \in [0, \pi]
$$
1.2.3 反正切函数(arctan(x))
反正切函数,记作 $\arctan(x)$,是正切函数的反函数。它的定义域为 $(-\infty, +\infty)$,值域为 $(-\frac{\pi}{2}, \frac{\pi}{2})$。即对于任意 $y = \arctan(x)$,有:
$$
\tan(y) = x, \quad y \in \left(-\frac{\pi}{2}, \frac{\pi}{2}\right)
$$
1.3 积化和差公式
$$
\sin(x \pm y) = \sin(x)\cos(y) \pm \cos(x)\sin(y)
$$
$$
\cos(x \pm y) = \cos(x)\cos(y) \mp \sin(x)\sin(y)
$$
$$
\tan(x \pm y) = \frac{\tan(x) \pm \tan(y)}{1 \mp \tan(x)\tan(y)}
$$
$$
\sin(x) \cos(y) = \frac{1}{2} \left[ \sin(x + y) + \sin(x - y) \right]
$$
$$
\cos(x) \sin(y) = \frac{1}{2} \left[ \sin(x + y) - \sin(x - y) \right]
$$
$$
\cos(x) \cos(y) = \frac{1}{2} \left[ \cos(x + y) + \cos(x - y) \right]
$$
$$
\sin(x) \sin(y) = \frac{1}{2} \left[ \cos(x - y) - \cos(x + y) \right]
$$
1.4 倍角/半角公式
$$
\sin(2x) = 2 \sin(x) \cos(x)
$$
$$
\cos(2x) = \cos^2(x) - \sin^2(x) = 2\cos^2(x) - 1 = 1 - 2\sin^2(x)
$$
$$
\tan(2x) = \frac{2\tan(x)}{1 - \tan^2(x)}
$$
$$
\sin\left(\frac{x}{2}\right) = \pm \sqrt{\frac{1 - \cos(x)}{2}}
$$
$$
\cos\left(\frac{x}{2}\right) = \pm \sqrt{\frac{1 + \cos(x)}{2}}
$$
$$
\tan\left(\frac{x}{2}\right) = \pm \sqrt{\frac{1 - \cos(x)}{1 + \cos(x)}} = \frac{\sin(x)}{1 + \cos(x)} = \frac{1 - \cos(x)}{\sin(x)}
$$
1.5 万能公式
设 $u = \tan\left(\frac{x}{2}\right)$,则有:
$$
\sin x = \frac{2u}{1 + u^2}, \quad x \in \left(-\frac{\pi}{2}, \frac{\pi}{2}\right)
$$
$$
\cos x = \frac{1 - u^2}{1 + u^2}, \quad x \in \left(-\frac{\pi}{2}, \frac{\pi}{2}\right)
$$
$$
\tan x = \frac{2u}{1 - u^2}, \quad x \in \left(-\frac{\pi}{2}, \frac{\pi}{2}\right)
$$
2. 一元二次方程
一元二次方程的标准形式是:
$$
ax^2 + bx + c = 0
$$
其中,$a$、$b$ 和 $c$ 是常数,且 $a \neq 0$。
一元二次方程的解的存在与否可以通过判别式 $\Delta$ 来判断,判别式的表达式是:
$$
\Delta = b^2 - 4ac
$$
根据 $\Delta$ 的值,可以判断方程的解的情况:
- 如果 $\Delta > 0$,方程有 两个不相等的实数解。
- 如果 $\Delta = 0$,方程有 一个实数解,也叫做 重根。
- 如果 $\Delta < 0$,方程没有实数解,只有 两个共轭复数解。
根据判别式 $\Delta$,方程的解可以通过求根公式来表示:
$$
x = \frac{-b \pm \sqrt{\Delta}}{2a}
$$
其中,“$\pm$”表示可以有两个解,分别是:
$$
x_1 = \frac{-b + \sqrt{\Delta}}{2a}, \quad x_2 = \frac{-b - \sqrt{\Delta}}{2a}
$$
- $\Delta = b^2 - 4ac$ 是判别式,它决定了方程解的个数和类型。
- 根据 $\Delta$ 的值,分别有不同的解的情况。
3. 等差/等比数列
3.1 等差数列的相关公式
等差数列是指每一项与前一项的差都相等的数列,常常用符号 $a_n$ 表示。
假设等差数列的首项为 $a_1$,公差为 $d$,则该数列的第 $n$ 项可以表示为:
$$
a_n = a_1 + (n - 1) d
$$
求和公式: 等差数列前 $n$ 项的和可以通过以下公式计算:
$$
S_n = \frac{n}{2} \left(2a_1 + (n - 1) d \right)
$$
或者
$$
S_n = \frac{n}{2} \left(a_1 + a_n \right)
$$
其中,$a_n$ 是数列的第 $n$ 项。
总结:
- 等差数列的第 $n$ 项公式:$a_n = a_1 + (n - 1)d$
- 等差数列前 $n$ 项的和公式:$S_n = \frac{n}{2} \left(2a_1 + (n - 1) d \right)$ 或者 $S_n = \frac{n}{2} \left(a_1 + a_n \right)$
3.2 等比数列的相关公式
等比数列是指每一项与前一项的比都相等的数列,常常用符号 $b_n$ 表示。
假设等比数列的首项为 $b_1$,公比为 $r$,则该数列的第 $n$ 项可以表示为:
$$
b_n = b_1 r^{n-1}
$$
求和公式: 等比数列前 $n$ 项的和可以通过以下公式计算:
- 当 $r \neq 1$ 时,前 $n$ 项的和为:
$$
S_n = \frac{b_1 (1 - r^n)}{1 - r}
$$
- 当 $r = 1$ 时,前 $n$ 项的和为:
$$
S_n = n \cdot b_1
$$
总结:
- 等比数列的第 $n$ 项公式:$b_n = b_1 r^{n-1}$
- 等比数列前 $n$ 项的和公式(当 $r \neq 1$):$S_n = \frac{b_1 (1 - r^n)}{1 - r}$
- 等比数列前 $n$ 项的和公式(当 $r = 1$):$S_n = n \cdot b_1$
4. 二项定理/组合数
二项式定理是用于展开 $(a + b)^n$ 的一个公式,它可以表示为:
$$
(a + b)^n = \sum_{k=0}^{n} \binom{n}{k} a^{n-k} b^k
$$
其中,$\binom{n}{k}$ 是 组合数,表示从 $n$ 个不同的元素中选取 $k$ 个元素的方式数。它的公式为:
$$
\binom{n}{k} = \frac{n!}{k!(n-k)!}
$$
组合数的性质:
- 对称性:
$$
\binom{n}{k} = \binom{n}{n-k}
$$
- 递推公式:
$$
\binom{n}{k} = \binom{n-1}{k-1} + \binom{n-1}{k}
$$
- 边界条件:
$$
\binom{n}{0} = 1, \quad \binom{n}{n} = 1
$$
- 与阶乘的关系:
$$
\binom{n}{k} = \frac{n!}{k!(n-k)!}
$$
二项式展开公式的应用:
二项式定理展开式中的每一项 $\binom{n}{k} a^{n-k} b^k$ 表示的是 $(a + b)^n$ 展开后的第 $k$ 项,其中 $\binom{n}{k}$ 是对应的组合数,它可以用来计算每一项的系数。
总结:
- 二项式定理展开式:$(a + b)^n = \sum_{k=0}^{n} \binom{n}{k} a^{n-k} b^k$
- 组合数公式:$\binom{n}{k} = \frac{n!}{k!(n-k)!}$
- 组合数的一些性质:
- $\binom{n}{k} = \binom{n}{n-k}$
- $\binom{n}{k} = \binom{n-1}{k-1} + \binom{n-1}{k}$
- $\binom{n}{0} = 1, \quad \binom{n}{n} = 1$
4.1 二项定理的证明
二项式定理的证明可以通过数学归纳法来进行,下面是详细的证明过程:
基本步骤:
我们希望证明对于任意自然数 $n$,都有:
$$
(a + b)^n = \sum_{k=0}^{n} \binom{n}{k} a^{n-k} b^k
$$
其中,$\binom{n}{k}$ 是组合数,表示从 $n$ 个元素中选出 $k$ 个元素的方法数。
1.归纳基础: $n = 0$
首先,我们验证当 $n = 0$ 时,公式是否成立:
对于 $n = 0$:
$$
(a + b)^0 = 1
$$
而右边的展开式为:
$$
\sum_{k=0}^{0} \binom{0}{k} a^{0-k} b^k = \binom{0}{0} a^0 b^0 = 1
$$
显然,当 $n = 0$ 时,公式成立。
2.归纳假设: 假设对于 $n = k$ 时成立
假设对于某个自然数 $k$,我们有:
$$
(a + b)^k = \sum_{i=0}^{k} \binom{k}{i} a^{k-i} b^i
$$
我们现在需要证明对于 $n = k+1$ 时,公式也成立。
3.归纳步骤: 证明 $n = k+1$ 时公式成立
考虑 $(a + b)^{k+1}$,我们可以将其分解为:
$$
(a + b)^{k+1} = (a + b)(a + b)^k
$$
根据归纳假设,$(a + b)^k$ 可以展开为:
$$
(a + b)^{k+1} = (a + b) \left( \sum_{i=0}^{k} \binom{k}{i} a^{k-i} b^i \right)
$$
接下来,展开右边的乘积:
$$
(a + b) \sum_{i=0}^{k} \binom{k}{i} a^{k-i} b^i = a \sum_{i=0}^{k} \binom{k}{i} a^{k-i} b^i + b \sum_{i=0}^{k} \binom{k}{i} a^{k-i} b^i
$$
将每项展开:
- 第一项是:
$$
a \sum_{i=0}^{k} \binom{k}{i} a^{k-i} b^i = \sum_{i=0}^{k} \binom{k}{i} a^{k+1-i} b^i
$$
- 第二项是:
$$
b \sum_{i=0}^{k} \binom{k}{i} a^{k-i} b^i = \sum_{i=0}^{k} \binom{k}{i} a^{k-i} b^{i+1}
$$
为了便于合并,我们将第二个求和的指标进行变换。令 $j = i+1$,则 $i = j-1$,且当 $i$ 从 $0$ 到 $k$ 变化时,$j$ 从 $1$ 到 $k+1$ 变化。因此:
$$
\sum_{i=0}^{k} \binom{k}{i} a^{k-i} b^{i+1} = \sum_{j=1}^{k+1} \binom{k}{j-1} a^{k-(j-1)} b^j = \sum_{j=1}^{k+1} \binom{k}{j-1} a^{k+1-j} b^j
$$
现在我们可以改写为:
$$
(a + b)^{k+1} = \sum_{i=0}^{k} \binom{k}{i} a^{k+1-i} b^i + \sum_{j=1}^{k+1} \binom{k}{j-1} a^{k+1-j} b^j
$$
为了合并这两个和式,我们将第一个和式的指标也改为 $j$。对于第一个和式,当 $i = j$,范围从 $0$ 到 $k$:
$$
(a + b)^{k+1} = \sum_{j=0}^{k} \binom{k}{j} a^{k+1-j} b^j + \sum_{j=1}^{k+1} \binom{k}{j-1} a^{k+1-j} b^j
$$
注意到:
- 在 $j=0$ 时,只有第一个和式有贡献,为 $\binom{k}{0}a^{k+1}b^0 = a^{k+1}$
- 在 $j=k+1$ 时,只有第二个和式有贡献,为 $\binom{k}{k}a^0b^{k+1} = b^{k+1}$
- 对于 $1 \leq j \leq k$,两个和式都有贡献
因此,我们可以将其重写为:
$$
(a + b)^{k+1} = \binom{k}{0}a^{k+1} + \sum_{j=1}^{k} \left( \binom{k}{j} + \binom{k}{j-1} \right) a^{k+1-j} b^j + \binom{k}{k}b^{k+1}
$$
根据组合数的递推关系(关键结论):$\binom{k+1}{j} = \binom{k}{j-1} + \binom{k}{j}$,上式可以写为:
$$
(a + b)^{k+1} = \binom{k+1}{0}a^{k+1} + \sum_{j=1}^{k} \binom{k+1}{j} a^{k+1-j} b^j + \binom{k+1}{k+1}b^{k+1}
$$
这可以进一步简化为:
$$
(a + b)^{k+1} = \sum_{j=0}^{k+1} \binom{k+1}{j} a^{k+1-j} b^j
$$
这正是我们需要的展开式,因此,二项式定理对于 $n = k+1$ 也成立。
4.结论
由归纳法可知,二项式定理对所有自然数 $n$ 都成立:
$$
(a + b)^n = \sum_{k=0}^{n} \binom{n}{k} a^{n-k} b^k
$$
5. 常见等价无穷小
在 $x \to 0$时,以下等价无穷小成立:
5.1. 基本等价无穷小
$$ \sin x \sim x $$
$$ \tan x \sim x $$
$$ \arcsin x \sim x $$
$$ \arctan x \sim x $$
$$ 1 - \cos x \sim \frac{x^2}{2} $$
$$ x - \sin x \sim \frac{x^3}{6} $$
$$ e^x - 1 \sim x $$
$$ \ln(1 + x) \sim x $$
5.2. 组合与扩展
$$ \ln(1 - x) \sim -x $$
$$ a^x - 1 \sim x \ln a \quad (a > 0, a \neq 1) $$
$$ (1 + x)^a - 1 \sim ax \quad (a \text{ 为常数}) $$
5.3. 其他常见形式
$$ \sqrt{1 + x} - 1 \sim \frac{x}{2} $$
$$ \frac{1}{1 + x} \sim 1 - x $$
6. 常见重要极限
在 $x \to 0$ 时,以下极限成立:
6.1. 经典初等极限
$$ \lim\limits_{x \to 0} \frac{\sin x}{x} = 1 $$
$$ \lim\limits_{x \to 0} \frac{\tan x}{x} = 1 $$
$$ \lim\limits_{x \to 0} \frac{\arcsin x}{x} = 1 $$
$$ \lim\limits_{x \to 0} \frac{\arctan x}{x} = 1 $$
$$ \lim\limits_{x \to 0} \frac{1 - \cos x}{x^2} = \frac{1}{2} $$
6.2. 指数与对数相关极限
$$ \lim\limits_{x \to 0} \frac{e^x - 1}{x} = 1 $$
$$ \lim\limits_{x \to 0} \frac{\ln(1 + x)}{x} = 1 $$
$$ \lim\limits_{x \to 0} \frac{\ln(1 - x)}{x} = -1 $$
$$ \lim\limits_{x \to \infty} \left( 1 + \frac{1}{x} \right)^x = e $$
$$ \lim\limits_{x \to 0} (1 + x)^{\frac{1}{x}} = e $$
6.3. 重要无穷小极限
$$ \lim\limits_{x \to 0} \frac{x - \sin x}{x^3} = \frac{1}{6} $$
$$ \lim\limits_{x \to 0} \frac{\tan x - x}{x^3} = \frac{1}{3} $$
$$ \lim\limits_{x \to 0} \frac{e^x - 1 - x}{x^2} = \frac{1}{2} $$
$$ \lim\limits_{x \to 0} \frac{\ln(1 + x) - x}{x^2} = -\frac{1}{2} $$
6.4. 其他重要极限
$$ \lim\limits_{x \to 0} \left( 1 + x \right)^{\frac{1}{x}} = e $$
$$ \lim\limits_{n \to \infty} \left( 1 + \frac{k}{n} \right)^n = e^k, \quad k \text{ 为常数} $$
$$ \lim\limits_{x \to 0} \frac{a^x - 1}{x} = \ln a, \quad (a > 0, a \neq 1) $$
7. 函数连续性
7.1. 极限存在
$$ \lim\limits_{x \to a} f(x) = L $$
极限存在是后续所有概念的基础。当函数 $f(x)$ 在点 $a$ 的邻域内有定义,且当 $x$ 无限接近 $a$ 时,函数值能够无限接近某个确定的常数 $L$,我们称该极限存在。
极限存在的条件:
- 左极限和右极限相等
- 极限值不依赖于函数在 $a$ 点的具体定义
- 可以通过 $\epsilon-\delta$ 语言严格定义
7.2. 连续
$$ \lim\limits_{x \to a} f(x) = f(a) $$
连续是对极限的进一步要求:
- 函数在点 $a$ 处有定义
- 极限存在
- 极限值等于函数在该点的函数值
连续的类型:
- 点连续
- 区间连续
- 一致连续
7.3. 可导(derivative)
$$ f’(a) = \lim\limits_{x \to a} \frac{f(x) - f(a)}{x - a} $$
可导是连续的进一步强化条件:
- 函数在点 $a$ 处连续
- 函数在点 $a$ 处存在唯一的切线
- 导数存在,表示函数在该点的瞬时变化率
可导的充要条件:
- 左导数和右导数存在且相等
7.4. 可微(differentiable)
$$ f(x + \Delta x) = f(x) + f’(x)\Delta x + o(\Delta x) $$
可微是可导的更强条件:
- 函数可导
- 在点 $a$ 处可以用线性函数进行局部近似
- 误差项 $o(\Delta x)$ 是高阶无穷小
可微的特点:
- 提供了函数局部线性逼近
- 在微积分和泰勒展开中有重要应用
7.5. 可偏导(partially differentiable)
$$ \frac{\partial f}{\partial x_i} = \lim\limits_{h \to 0} \frac{f(x_1, \ldots, x_i + h, \ldots, x_n) - f(x_1, \ldots, x_n)}{h} $$
可偏导是多变量函数的导数概念:
- 定义在多元函数上
- 固定其他变量,对某一变量求导
- 每个自变量都存在偏导数
可偏导的条件:
- 每个方向的导数都存在
- 不要求所有偏导数连续
7.6 关系总结
极限存在 $\Rightarrow$ 连续
- 极限存在是连续的必要条件
- 但极限存在不一定保证连续
连续 $\Rightarrow$ 可导
- 连续是可导的必要条件
- 但连续不一定保证可导
可导 $\Rightarrow$ 可微
- 可导是可微的必要条件
- 可导函数一定可微
可导 $\Rightarrow$ 连续
- 可导函数一定连续
- 连续是可导的必要条件
多元函数的可偏导
- 要求每个方向的导数存在
- 不要求偏导数连续或存在
典型反例
- $f(x) = |x|$ 在 $x = 0$ 处连续但不可导
- $f(x) = x \sin(\frac{1}{x})$($x \neq 0$)在 $x = 0$ 处极限存在但不连续

考虑函数:
$$
f(x) = \begin{cases}
x \sin\left(\frac{1}{x}\right), & x \ne 0 \\
0, & x = 0
\end{cases}
$$
我们想研究它在 $x = 0$ 处的极限是否存在,以及是否连续。
第一步:计算 $\displaystyle \lim_{x \to 0} x \sin\left(\frac{1}{x}\right)$ 是否存在
分析:
- $\sin\left(\frac{1}{x}\right)$ 在 $x \to 0$ 时没有极限,因为 $\frac{1}{x}$ 趋向于无穷大,$\sin$ 在 $[-1, 1]$ 之间来回震荡,没有收敛。
- 但是,$x$ 趋近于 $0$,我们可以尝试夹逼准则(夹挤准则):
$$
\lim_{x \to 0} x \sin\left(\frac{1}{x}\right) = 0
$$
第二步:分析函数在 $x = 0$ 处是否连续
连续的定义是:
$$
\lim_{x \to 0} f(x) = f(0)
$$
我们刚才算出极限是 $0$,而题目中也定义 $f(0) = 0$,看起来似乎是连续?
但 小心!
上面我们讨论的是 $x \sin(1/x)$ 的极限存在为 $0$,所以如果我们定义 $f(0) = 0$,那么函数就连续!
而如果我们定义 $f(0)$ 为其它数,比如没有定义或者定义为 $1$,那函数就不连续了。
那为什么有时候说这个函数“极限存在但不连续”?
这是因为有时候题目只给你 $f(x) = x \sin\left(\frac{1}{x}\right)$,但没有定义 $f(0)$,也就是说函数在 $x=0$ 处没有定义,你只能讨论极限是否存在,不能说连续不连续。
最终结论:
- $f(x) = x \sin\left(\frac{1}{x}\right)$ 的极限在 $x=0$ 处是存在的,值为 $0$。
- 若定义 $f(0) = 0$,则该函数在 $x = 0$ 连续。
- 若 $f(0)$ 没定义,或者定义为不等于 0 的值,那么函数在 $x=0$ 极限存在但不连续。
8. 常见函数的导数
8.1. 基本初等函数的导数
$$ (C)’ = 0, \quad C \text{ 为常数} $$
$$ (x^n)’ = nx^{n-1} $$
$$ (e^x)’ = e^x $$
$$ (\ln x)’ = \frac{1}{x} $$
$$ (\sin x)’ = \cos x $$
$$ (\cos x)’ = -\sin x $$
$$ (\tan x)’ = \sec^2 x $$
$$ (\cot x)’ = -\csc^2 x $$
$$ (\sec x)’ = \sec x \tan x $$
$$ (\csc x)’ = -\csc x \cot x $$
8.2. 反三角函数的导数
$$ (\arcsin x)’ = \frac{1}{\sqrt{1-x^2}} $$
$$ (\arccos x)’ = -\frac{1}{\sqrt{1-x^2}} $$
$$ (\arctan x)’ = \frac{1}{1+x^2} $$
$$ (\text{arccot } x)’ = -\frac{1}{1+x^2} $$
$$ (\text{arcsec } x)’ = \frac{1}{|x|\sqrt{x^2-1}} $$
$$ (\text{arccsc } x)’ = -\frac{1}{|x|\sqrt{x^2-1}} $$
8.3. 指数与对数函数的导数
$$ (a^x)’ = a^x \ln a, \quad (a > 0, a \neq 1) $$
$$ (\log_a x)’ = \frac{1}{x \ln a}, \quad (a > 0, a \neq 1) $$
8.4. 复合函数、积、商的导数
$$ [f(g(x))]’ = f’(g(x)) \cdot g’(x) $$
$$ (u \cdot v)’ = u’ \cdot v + u \cdot v’ $$
$$ \left(\frac{u}{v}\right)’ = \frac{u’ \cdot v - u \cdot v’}{v^2} $$
8.5. 双曲函数的导数
$$ (\sinh x)’ = \cosh x $$
$$ (\cosh x)’ = \sinh x $$
$$ (\tanh x)’ = \text{sech}^2 x $$
$$ (\coth x)’ = -\text{csch}^2 x $$
$$ (\text{sech } x)’ = -\text{sech } x \tanh x $$
$$ (\text{csch } x)’ = -\text{csch } x \coth x $$
9. 常见不等式
9.1. 基本不等式
$$ a \geq b \Rightarrow a^n \geq b^n, \quad (a,b > 0, n > 0) $$
$$ |a + b| \leq |a| + |b| $$
$$ |a - b| \geq \left| |a| - |b| \right| $$
$$ \frac{a+b}{2} \geq \sqrt{ab}, \quad (a,b > 0) $$
$$ \frac{a_1 + a_2 + \cdots + a_n}{n} \geq \sqrt[n]{a_1 a_2 \cdots a_n}, \quad (a_i > 0) $$
9.2. 三角函数不等式
$$ \sin x < x < \tan x, \quad (0 < x < \frac{\pi}{2}) $$
$$ \sin x \geq \frac{2x}{\pi}, \quad (0 \leq x \leq \frac{\pi}{2}) $$
$$ \cos x \geq 1 - \frac{x^2}{2}, \quad (x \in \mathbb{R}) $$
$$ |\sin x| \leq |x|, \quad (x \in \mathbb{R}) $$
$$ 1 - \cos x \leq \frac{x^2}{2}, \quad (x \in \mathbb{R}) $$
9.3. 指数与对数不等式
$$ e^x \geq 1 + x, \quad (x \in \mathbb{R}) $$
$$ e^x \geq 1 + x + \frac{x^2}{2}, \quad (x \geq 0) $$
$$ \ln(1+x) \leq x, \quad (x > -1) $$
$$ \ln x \leq x - 1, \quad (x > 0) $$
$$ x^a < x^b, \quad (0 < x < 1, a > b) $$
$$ x^a > x^b, \quad (x > 1, a > b) $$
9.4. 柯西不等式与其扩展
$$ \left( \sum_{i=1}^{n} a_i b_i \right)^2 \leq \left( \sum_{i=1}^{n} a_i^2 \right) \left( \sum_{i=1}^{n} b_i^2 \right) $$
$$ \left( \frac{a_1 + a_2 + \cdots + a_n}{n} \right)^2 \leq \frac{a_1^2 + a_2^2 + \cdots + a_n^2}{n} $$
$$ \frac{1}{a_1} + \frac{1}{a_2} + \cdots + \frac{1}{a_n} \geq \frac{n^2}{a_1 + a_2 + \cdots + a_n}, \quad (a_i > 0) $$
9.5. 经典不等式
$$ \frac{a^n + b^n}{2} \geq \left( \frac{a + b}{2} \right)^n, \quad (a, b > 0, n \geq 1) $$
$$ \frac{a^n + b^n}{2} \leq \left( \frac{a + b}{2} \right)^n, \quad (a, b > 0, 0 < n < 1) $$
$$ a^b \cdot b^a \leq a^a \cdot b^b, \quad (a, b > 0) $$
$$ \sqrt{1+x} < 1 + \frac{x}{2}, \quad (x > 0) $$
$$ (1+x)^n \geq 1 + nx, \quad (x > -1, n > 1) $$
10. 函数凹凸性
10.1. 函数的凹凸性定义
凸函数(上凸函数): 若函数 $f(x)$ 在区间 $I$ 内满足:
$$ f(\lambda x_1 + (1 - \lambda)x_2) \leq \lambda f(x_1) + (1 - \lambda) f(x_2), \quad (\lambda \in [0,1]) $$
则称 $f(x)$ 在 $I$ 上是凸函数(Convex Function)。
凹函数(下凸函数): 若函数 $f(x)$ 在区间 $I$ 内满足:
$$ f(\lambda x_1 + (1 - \lambda)x_2) \geq \lambda f(x_1) + (1 - \lambda) f(x_2), \quad (\lambda \in [0,1]) $$
则称 $f(x)$ 在 $I$ 上是凹函数(Concave Function)。
几何上,凸函数的图像在任意两点之间的弦线之下,凹函数的图像在弦线之上。
10.2. 通过二阶导数判断凹凸性
若 $f(x)$ 在区间 $I$ 二阶可导,则:
- 若 $f’’(x) > 0$,则 $f(x)$ 在 $I$ 上凸(凸函数);
- 若 $f’’(x) < 0$,则 $f(x)$ 在 $I$ 下凸(凹函数);
- 若 $f’’(x) = 0$,需要进一步分析高阶导数或函数的局部行为。
示例:
- $f(x) = x^2$,二阶导数 $f’’(x) = 2 > 0$,是凸函数(向上弯曲)。
- $f(x) = -x^2$,二阶导数 $f’’(x) = -2 < 0$,是凹函数(向下弯曲)。
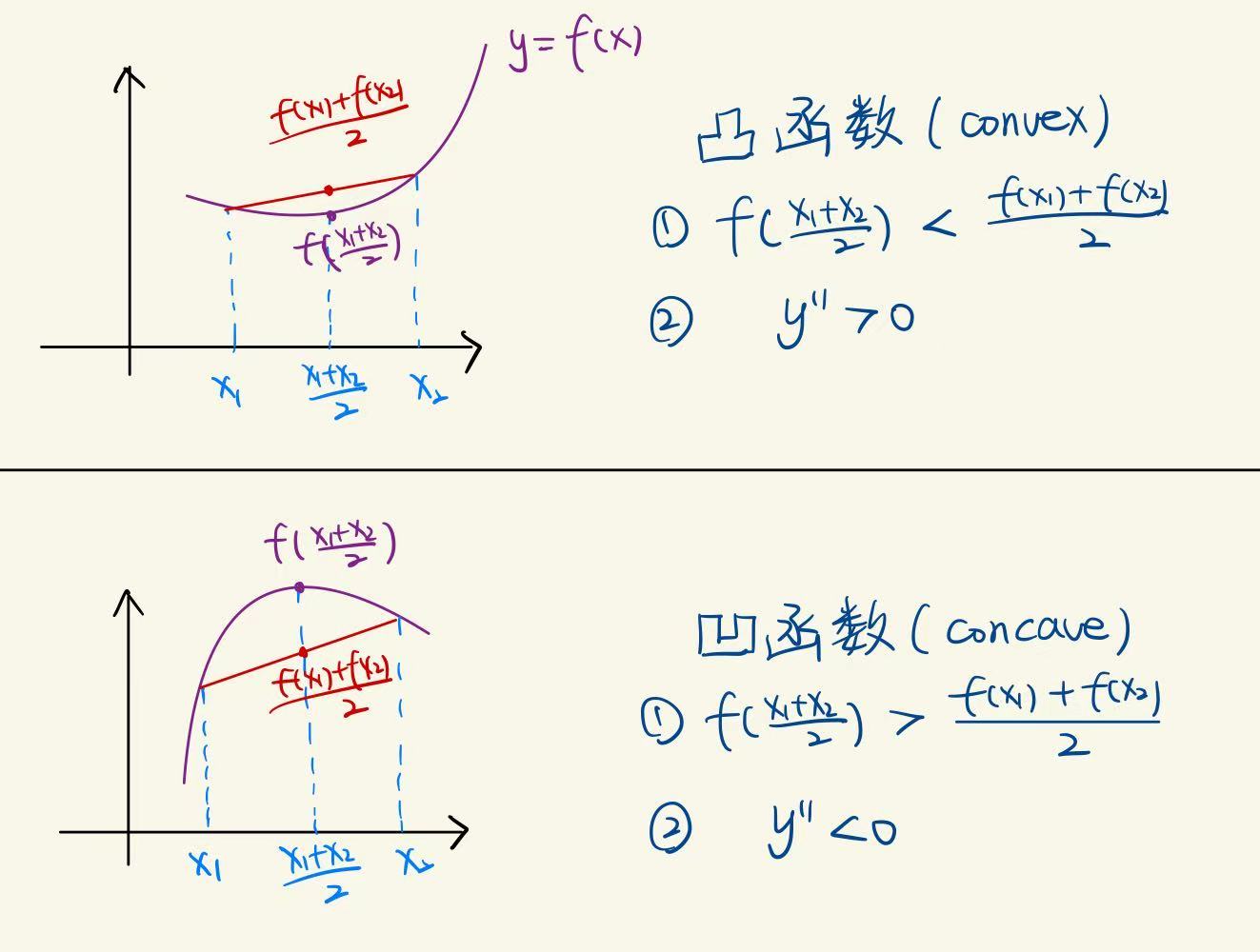
⚠️注意国内定义的凹凸性和国际上的凹凸性是反过来的…这里以国际定义为准
10.3. 拐点(Inflection Point)
若 $f(x)$ 的二阶导数在某点 $x = c$ 发生符号变化,即满足:
$$ f’’(c) = 0, \quad \text{且} \quad f’’(x) \text{ 在 } c \text{ 处改变符号} $$
则称 $x = c$ 为函数的拐点,即函数从凸变凹或从凹变凸的点。
示例:
- $f(x) = x^3$,二阶导数 $f’’(x) = 6x$,在 $x = 0$ 处由负变正,因此 $x = 0$ 是拐点。
10.4. 经典结论
- 指数函数 $f(x) = e^x$,二阶导数 $f’’(x) = e^x > 0$,是凸函数。
- 对数函数 $f(x) = \ln x$,二阶导数 $f’’(x) = -\frac{1}{x^2} < 0$,是凹函数。
- 幂函数 $f(x) = x^p$:
- 若 $p \geq 1$ 或 $0 < p < 1$,则 $f(x)$ 在 $x > 0$ 上是凸函数。
- 若 $p < 0$,则 $f(x)$ 在 $x > 0$ 上是凹函数。
10.5. 例题解析
例 1:判断函数 $f(x) = x^4 - 4x^3 + 6x^2$ 的凹凸性及拐点
解:
一阶导数:
$$ f’(x) = 4x^3 - 12x^2 + 12x $$
二阶导数:
$$ f’’(x) = 12x^2 - 24x + 12 $$
令 $f’’(x) = 0$ 求拐点:
$$ 12(x^2 - 2x + 1) = 0 $$
$$ 12(x - 1)^2 = 0 \Rightarrow x = 1 $$
由于 $f’’(x)$ 在 $x = 1$ 两侧符号没有变化,说明函数在整个定义域内都是凸的。
10.6. 重要不等式
Jensen 不等式(对凸函数成立):
$$ f\left(\frac{x_1 + x_2}{2}\right) \leq \frac{f(x_1) + f(x_2)}{2} $$
若 $f(x)$ 是凹函数,则不等号方向相反。
均值不等式(对幂函数成立):
$$ \frac{a^n + b^n}{2} \geq \left( \frac{a + b}{2} \right)^n, \quad (a, b > 0, n \geq 1) $$
$$ \frac{a^n + b^n}{2} \leq \left( \frac{a + b}{2} \right)^n, \quad (a, b > 0, 0 < n < 1) $$
指数与对数的不等式(由凹凸性推出):
$$ a^b \cdot b^a \leq a^a \cdot b^b, \quad (a, b > 0) $$
$$ \sqrt{1+x} < 1 + \frac{x}{2}, \quad (x > 0) $$
$$ (1+x)^n \geq 1 + nx, \quad (x > -1, n > 1) $$
10.7. 总结
- 凸函数满足 $f’’(x) > 0$,图像向上弯曲。
- 凹函数满足 $f’’(x) < 0$,图像向下弯曲。
- 拐点是函数从凹变凸或从凸变凹的点,满足 $f’’(x) = 0$ 且符号发生变化。
- 经典结论:
- $e^x$ 是凸函数
- $\ln x$ 是凹函数
- $x^p$ 的凹凸性取决于 $p$ 的大小
10.8. Jesen不等式
Jensen不等式的基本形式
$$ \varphi\left(\sum_{i=1}^n \lambda_i x_i\right) \leq \sum_{i=1}^n \lambda_i \varphi(x_i), \quad (\varphi \text{ 为凸函数}) $$
$$ \varphi\left(\sum_{i=1}^n \lambda_i x_i\right) \geq \sum_{i=1}^n \lambda_i \varphi(x_i), \quad (\varphi \text{ 为凹函数}) $$
$$ \text{其中} \sum_{i=1}^n \lambda_i = 1, \lambda_i \geq 0, i=1,2,\ldots,n $$
等号成立当且仅当满足以下任一条件:
$x_1 = x_2 = \cdots = x_n$
即所有的 $x_i$ 都相等。
$\varphi(x) \text{ 在包含所有 } x_i \text{ 的区间上是线性函数}$ 即 $\varphi(x) = ax + b$,其中 $a, b$ 为常数。
这两个条件可以这样理解:
当所有点 $x_i$ 相同时,无论权重 $\lambda_i$ 如何分配,加权平均值都等于这个公共值,因此等号成立。
当 $\varphi(x)$ 是线性函数时,它既不是严格凸的也不是严格凹的($\varphi’’(x) = 0$),这种情况下,函数值的加权平均恰好等于函数在加权平均点的值,从而等号成立。
对于严格凸函数($\varphi’’(x) > 0$)或严格凹函数($\varphi’’(x) < 0$),等号成立当且仅当所有 $x_i$ 都相等。
连续形式的Jensen不等式
$$ \varphi\left(\int_a^b f(x) g(x) dx\right) \leq \int_a^b \varphi(f(x)) g(x) dx, \quad (\varphi \text{ 为凸函数}) $$
$$ \varphi\left(\int_a^b f(x) g(x) dx\right) \geq \int_a^b \varphi(f(x)) g(x) dx, \quad (\varphi \text{ 为凹函数}) $$
$$ \text{其中} \int_a^b g(x) dx = 1, g(x) \geq 0 $$
概率形式的Jensen不等式
$$ \varphi(E[X]) \leq E[\varphi(X)], \quad (\varphi \text{ 为凸函数}) $$
$$ \varphi(E[X]) \geq E[\varphi(X)], \quad (\varphi \text{ 为凹函数}) $$
$$ \text{其中} E[X] \text{ 表示随机变量 } X \text{ 的期望} $$
典型应用案例
$$ \left(\frac{a_1 + a_2 + \cdots + a_n}{n}\right)^p \leq \frac{a_1^p + a_2^p + \cdots + a_n^p}{n}, \quad (a_i > 0, p > 1) $$
$$ \left(\frac{a_1 + a_2 + \cdots + a_n}{n}\right)^p \geq \frac{a_1^p + a_2^p + \cdots + a_n^p}{n}, \quad (a_i > 0, 0 < p < 1) $$
$$ \ln\left(\frac{a_1 + a_2 + \cdots + a_n}{n}\right) \geq \frac{\ln a_1 + \ln a_2 + \cdots + \ln a_n}{n}, \quad (a_i > 0) $$
Jensen不等式的几何解释
$$ \varphi(tx_1 + (1-t)x_2) \leq t\varphi(x_1) + (1-t)\varphi(x_2), \quad (0 \leq t \leq 1, \varphi \text{ 为凸函数}) $$
$$ \varphi(tx_1 + (1-t)x_2) \geq t\varphi(x_1) + (1-t)\varphi(x_2), \quad (0 \leq t \leq 1, \varphi \text{ 为凹函数}) $$
$$ \text{即凸函数图像上任意两点的连线位于图像上方,凹函数则位于图像下方} $$
严格不等式条件
$$ \varphi\left(\sum_{i=1}^n \lambda_i x_i\right) < \sum_{i=1}^n \lambda_i \varphi(x_i), \quad (\varphi \text{ 为严格凸函数且不是所有 } x_i \text{ 都相等}) $$
$$ \varphi\left(\sum_{i=1}^n \lambda_i x_i\right) > \sum_{i=1}^n \lambda_i \varphi(x_i), \quad (\varphi \text{ 为严格凹函数且不是所有 } x_i \text{ 都相等}) $$
11. 泰勒公式&麦克劳林公式
11.1 泰勒公式
泰勒公式是一种用多项式函数近似表示光滑函数的方法。它使我们能够在某点附近用幂级数展开函数。
假设函数 $f(x)$ 在点 $x=a$ 的某个邻域内具有 $n+1$ 阶连续导数,那么对于该邻域内的任意点 $x$,函数 $f(x)$ 可以表示为:
$$ f(x) = f(a) + f’(a)(x-a) + \frac{f’’(a)}{2!}(x-a)^2 + \cdots + \frac{f^{(n)}(a)}{n!}(x-a)^n + R_n(x) $$
其中 $R_n(x)$ 是拉格朗日余项,表示为:
$$ R_n(x) = \frac{f^{(n+1)}(\xi)}{(n+1)!}(x-a)^{n+1} $$
这里 $\xi$ 是介于 $a$ 和 $x$ 之间的某个值。
泰勒公式的另一种常见形式是带有皮亚诺余项:
$$ f(x) = f(a) + f’(a)(x-a) + \frac{f’’(a)}{2!}(x-a)^2 + \cdots + \frac{f^{(n)}(a)}{n!}(x-a)^n + o((x-a)^n) $$
11.2 麦克劳林公式
麦克劳林公式是泰勒公式的特殊情况,即在点 $a=0$ 处展开:
$$ f(x) = f(0) + f’(0)x + \frac{f’’(0)}{2!}x^2 + \cdots + \frac{f^{(n)}(0)}{n!}x^n + R_n(x) $$
其中余项 $R_n(x)$ 表示为:
$$ R_n(x) = \frac{f^{(n+1)}(\xi)}{(n+1)!}x^{n+1} $$
这里 $\xi$ 是介于 $0$ 和 $x$ 之间的某个值。
让我们看一个例子,计算 $\sin(0.1)$ 的近似值:
使用麦克劳林公式展开到 $x^5$ 项:
$$ \sin(0.1) \approx 0.1 - \frac{(0.1)^3}{3!} + \frac{(0.1)^5}{5!} $$
$$ \sin(0.1) \approx 0.1 - \frac{0.001}{6} + \frac{0.00001}{120} $$
$$ \sin(0.1) \approx 0.1 - 0.000167 + 0.000000083 \approx 0.099833 $$
实际值 $\sin(0.1) \approx 0.0998334$,所以这个近似是相当准确的。
11.3 常见函数的麦克劳林展开
以下是一些常见函数的麦克劳林展开式:
指数函数:
$$ e^x = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \cdots = \sum_{n=0}^{\infty} \frac{x^n}{n!} $$正弦函数:
$$ \sin x = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \cdots = \sum_{n=0}^{\infty} \frac{(-1)^n x^{2n+1}}{(2n+1)!} $$余弦函数:
$$ \cos x = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \cdots = \sum_{n=0}^{\infty} \frac{(-1)^n x^{2n}}{(2n)!} $$自然对数函数:
$$ \ln(1+x) = x - \frac{x^2}{2} + \frac{x^3}{3} - \cdots = \sum_{n=1}^{\infty} \frac{(-1)^{n+1}x^n}{n}, \quad |x| < 1 $$反正切函数:
$$ \arctan x = x - \frac{x^3}{3} + \frac{x^5}{5} - \frac{x^7}{7} + \cdots = \sum_{n=0}^{\infty} \frac{(-1)^n x^{2n+1}}{2n+1}, \quad |x| \leq 1 $$双曲正弦函数:
$$ \sinh x = x + \frac{x^3}{3!} + \frac{x^5}{5!} + \cdots = \sum_{n=0}^{\infty} \frac{x^{2n+1}}{(2n+1)!} $$双曲余弦函数:
$$ \cosh x = 1 + \frac{x^2}{2!} + \frac{x^4}{4!} + \cdots = \sum_{n=0}^{\infty} \frac{x^{2n}}{(2n)!} $$$(1+x)^{\alpha}$ 的二项式展开(广义二项式定理):
$$ (1+x)^{\alpha} = 1 + \alpha x + \frac{\alpha(\alpha-1)}{2!}x^2 + \frac{\alpha(\alpha-1)(\alpha-2)}{3!}x^3 + \cdots, \quad |x| < 1 $$
$$ = \sum_{n=0}^{\infty} \binom{\alpha}{n} x^n, \quad |x| < 1 $$
其中 $\binom{\alpha}{n} = \frac{\alpha(\alpha-1)(\alpha-2)\cdots(\alpha-n+1)}{n!}$正切函数:
$$ \tan x = x + \frac{x^3}{3} + \frac{2x^5}{15} + \frac{17x^7}{315} + \cdots, \quad |x| < \frac{\pi}{2} $$反正弦函数:
$$ \arcsin x = x + \frac{1}{2} \cdot \frac{x^3}{3} + \frac{1 \cdot 3}{2 \cdot 4} \cdot \frac{x^5}{5} + \frac{1 \cdot 3 \cdot 5}{2 \cdot 4 \cdot 6} \cdot \frac{x^7}{7} + \cdots, \quad |x| \leq 1 $$平方根函数:
$$ \sqrt{1+x} = 1 + \frac{1}{2}x - \frac{1}{8}x^2 + \frac{1}{16}x^3 - \frac{5}{128}x^4 + \cdots, \quad |x| < 1 $$倒数函数:
$$ \frac{1}{1-x} = 1 + x + x^2 + x^3 + \cdots = \sum_{n=0}^{\infty} x^n, \quad |x| < 1 $$双曲正切函数:
$$ \tanh x = x - \frac{x^3}{3} + \frac{2x^5}{15} - \frac{17x^7}{315} + \cdots, \quad |x| < \frac{\pi}{2} $$余切函数级数:
$$ \cot x = \frac{1}{x} - \frac{x}{3} - \frac{x^3}{45} - \frac{2x^5}{945} - \cdots, \quad 0 < |x| < \pi $$正割函数:
$$ \sec x = 1 + \frac{x^2}{2} + \frac{5x^4}{24} + \frac{61x^6}{720} + \cdots, \quad |x| < \frac{\pi}{2} $$
11.4 复合函数的麦克劳林展开
$e^{-x^2}$ 的麦克劳林展开:
$$ e^{-x^2} = 1 - x^2 + \frac{x^4}{2!} - \frac{x^6}{3!} + \cdots = \sum_{n=0}^{\infty} \frac{(-1)^n x^{2n}}{n!} $$$\ln(1-x)$ 的麦克劳林展开:
$$ \ln(1-x) = -x - \frac{x^2}{2} - \frac{x^3}{3} - \frac{x^4}{4} - \cdots = -\sum_{n=1}^{\infty} \frac{x^n}{n}, \quad |x| < 1 $$$\frac{1}{(1-x)^2}$ 的麦克劳林展开:
$$ \frac{1}{(1-x)^2} = 1 + 2x + 3x^2 + 4x^3 + \cdots = \sum_{n=0}^{\infty} (n+1)x^n, \quad |x| < 1 $$
12. 常见积分的基本公式
12.1. 基本不定积分公式
常数积分:
$$ \int k , dx = kx + C $$幂函数积分:
$$ \int x^n , dx = \frac{x^{n+1}}{n+1} + C, \quad (n \neq -1) $$对数函数积分:
$$ \int \frac{1}{x} , dx = \ln|x| + C $$指数函数积分:
$$ \int e^x , dx = e^x + C $$
$$ \int a^x , dx = \frac{a^x}{\ln a} + C, \quad (a > 0, a \neq 1) $$三角函数积分:
$$ \int \sin x , dx = -\cos x + C $$
$$ \int \cos x , dx = \sin x + C $$
$$ \int \tan x , dx = -\ln|\cos x| + C = \ln|\sec x| + C $$
$$ \int \cot x , dx = \ln|\sin x| + C $$
$$ \int \sec x , dx = \ln|\sec x + \tan x| + C $$
$$ \int \csc x , dx = \ln|\csc x - \cot x| + C = \ln|\tan(x/2)| + C $$反三角函数积分:
$$ \int \frac{1}{\sqrt{1-x^2}} , dx = \arcsin x + C = -\arccos x + C $$
$$ \int \frac{1}{1+x^2} , dx = \arctan x + C $$
$$ \int \frac{1}{|x|\sqrt{x^2-1}} , dx = \arccos\frac{1}{|x|} + C $$双曲函数积分:
$$ \int \sinh x , dx = \cosh x + C $$
$$ \int \cosh x , dx = \sinh x + C $$
$$ \int \tanh x , dx = \ln(\cosh x) + C $$
$$ \int \coth x , dx = \ln|\sinh x| + C $$
12.2. 特殊形式积分
分式积分:
$$ \int \frac{1}{a^2+x^2} , dx = \frac{1}{a}\arctan\frac{x}{a} + C, \quad (a > 0) $$
$$ \int \frac{1}{a^2-x^2} , dx = \frac{1}{2a}\ln\left|\frac{a+x}{a-x}\right| + C, \quad (|x| < a) $$
$$ \int \frac{1}{x^2-a^2} , dx = \frac{1}{2a}\ln\left|\frac{x-a}{x+a}\right| + C, \quad (|x| > a) $$根式积分:
$$ \int \frac{1}{\sqrt{a^2-x^2}} , dx = \arcsin\frac{x}{a} + C, \quad (|x| < a, a > 0) $$
$$ \int \frac{1}{\sqrt{x^2-a^2}} , dx = \ln|x + \sqrt{x^2-a^2}| + C, \quad (x > a > 0) $$
$$ \int \frac{1}{\sqrt{x^2+a^2}} , dx = \ln|x + \sqrt{x^2+a^2}| + C, \quad (a > 0) $$
$$ \int \sqrt{a^2-x^2} , dx = \frac{x\sqrt{a^2-x^2}}{2} + \frac{a^2}{2}\arcsin\frac{x}{a} + C, \quad (|x| < a, a > 0) $$
$$ \int \sqrt{x^2+a^2} , dx = \frac{x\sqrt{x^2+a^2}}{2} + \frac{a^2}{2}\ln|x + \sqrt{x^2+a^2}| + C, \quad (a > 0) $$
$$ \int \sqrt{x^2-a^2} , dx = \frac{x\sqrt{x^2-a^2}}{2} - \frac{a^2}{2}\ln|x + \sqrt{x^2-a^2}| + C, \quad (x > a > 0) $$特殊乘积结构:
$$ \int x\sin x , dx = \sin x - x\cos x + C $$
$$ \int x\cos x , dx = \cos x + x\sin x + C $$
$$ \int x^n e^x , dx = x^n e^x - n\int x^{n-1}e^x , dx $$
$$ \int x^n \ln x , dx = \frac{x^{n+1}}{n+1}\ln x - \frac{x^{n+1}}{(n+1)^2} + C, \quad (n \neq -1) $$有理三角函数变形:
$$ \int \sin^2 x , dx = \frac{x}{2} - \frac{\sin 2x}{4} + C $$
$$ \int \cos^2 x , dx = \frac{x}{2} + \frac{\sin 2x}{4} + C $$
$$ \int \sin^n x , dx = -\frac{\sin^{n-1}x \cos x}{n} + \frac{n-1}{n}\int \sin^{n-2}x , dx, \quad (n > 1) $$
$$ \int \cos^n x , dx = \frac{\cos^{n-1}x \sin x}{n} + \frac{n-1}{n}\int \cos^{n-2}x , dx, \quad (n > 1) $$平方和与差的积分:
$$ \int \frac{1}{x^2+a^2} , dx = \frac{1}{a}\arctan\frac{x}{a} + C, \quad (a > 0) $$
$$ \int \frac{x}{x^2+a^2} , dx = \frac{1}{2}\ln(x^2+a^2) + C $$
$$ \int \frac{x^2}{x^2+a^2} , dx = x - a\arctan\frac{x}{a} + C, \quad (a > 0) $$
12.3. 特殊定积分
常见定积分:
$$ \int_0^{\pi/2} \sin^n x , dx = \int_0^{\pi/2} \cos^n x , dx = \begin{cases}
\frac{(n-1)!!}{n!!} \cdot \frac{\pi}{2}, & \text{n 为偶数} \
\frac{(n-1)!!}{n!!}, & \text{n 为奇数}
\end{cases} $$
其中 $n!! = n(n-2)(n-4)\cdots$对称区间上的奇偶性质:
$$ \int_{-a}^{a} f(x) , dx = 2\int_0^a f(x) , dx, \quad \text{当 } f \text{ 为偶函数} $$
$$ \int_{-a}^{a} f(x) , dx = 0, \quad \text{当 } f \text{ 为奇函数} $$华里士公式:
$$ \int_0^{\pi/2} \sin^m x \cos^n x , dx = \frac{1}{2}B\left(\frac{m+1}{2}, \frac{n+1}{2}\right) = \frac{\Gamma\left(\frac{m+1}{2}\right)\Gamma\left(\frac{n+1}{2}\right)}{2\Gamma\left(\frac{m+n+2}{2}\right)} $$
其中 $B$ 是贝塔函数,$\Gamma$ 是伽马函数$\Gamma$ 函数相关积分:
$$ \int_0^{\infty} x^{n-1}e^{-x} , dx = \Gamma(n), \quad (n > 0) $$
$$ \int_0^{\infty} e^{-x^2} , dx = \frac{\sqrt{\pi}}{2} $$重要极限类型定积分:
$$ \lim_{n \to \infty} \int_0^1 (1-x^n)^n , dx = \frac{1}{e} $$
$$ \lim_{n \to \infty} \int_0^{\infty} \frac{x^n}{n^{n+1}} e^{-x/n} , dx = 1 $$
12.4. 换元积分法的典型例子
三角换元:
$$ \int \sqrt{a^2-x^2} , dx = \frac{a^2}{2}\arcsin\frac{x}{a} + \frac{x\sqrt{a^2-x^2}}{2} + C, \quad (|x| < a) $$
(令 $x = a\sin t$)双曲换元:
$$ \int \sqrt{x^2+a^2} , dx = \frac{x\sqrt{x^2+a^2}}{2} + \frac{a^2}{2}\ln|x + \sqrt{x^2+a^2}| + C $$
(令 $x = a\sinh t$)有理分式积分:
$$ \int \frac{1}{(x-a)(x-b)} , dx = \frac{1}{a-b}\ln\left|\frac{x-a}{x-b}\right| + C, \quad (a \neq b) $$
$$ \int \frac{1}{(x-a)^2} , dx = -\frac{1}{x-a} + C $$
13. Gamma函数
1. Gamma 函数的定义
Gamma 函数的基本定义为:
$$
\Gamma(x) = \int_0^\infty t^{x-1} e^{-t} , dt, \quad x > 0
$$
它是阶乘的连续扩展,并且在所有正实数 $x$ 上收敛。
2. Gamma 函数与阶乘的关系
Gamma 函数在正整数点满足:
$$
\Gamma(n) = (n-1)!
$$
即对于任意正整数 $n$:
$$
\Gamma(n) = \int_0^\infty t^{n-1} e^{-t} , dt = (n-1)!
$$
这表明 Gamma 函数是阶乘的推广,使得非整数的阶乘也可以计算。
3. Gamma 函数的性质
(1) 递推关系
$$
\Gamma(x+1) = x \Gamma(x)
$$
这类似于阶乘的递推公式:
$$
n! = n \times (n-1)!
$$
但适用于所有实数 $x$。
(2) 特殊值
$$
\Gamma(1) = \int_0^\infty e^{-t} dt = 1
$$
$$
\Gamma\left(\frac{1}{2}\right) = \sqrt{\pi}
$$
(3) 反射公式(欧拉反射公式)
$$
\Gamma(x) \Gamma(1-x) = \frac{\pi}{\sin(\pi x)}
$$
这在计算某些特殊值时非常有用。
(4) 斯特林近似公式
对于 $x \to \infty$,Gamma 函数可以近似为:
$$
\Gamma(x) \approx \sqrt{2\pi} x^{x-\frac{1}{2}} e^{-x}
$$
这表明它在大数时的增长速度类似于阶乘。
4. Gamma 函数的应用
(1) 在概率统计中的应用
Gamma 分布的概率密度函数:
$$
f(x; k, \theta) = \frac{x^{k-1} e^{-x/\theta}}{\theta^k \Gamma(k)}
$$
在贝叶斯统计、可靠性分析等领域有重要作用。
(2) 在积分计算中的应用
一个重要的积分公式:
$$
\int_0^\infty x^{s-1} e^{-ax} dx = \frac{\Gamma(s)}{a^s}, \quad a > 0
$$
这在傅里叶变换、Laplace 变换等领域广泛使用。
(3) 物理学中的应用
Gamma 函数出现在玻尔兹曼统计、量子场论等许多物理理论中。例如,在统计物理中,配分函数的计算可能涉及 Gamma 函数。
5. Gamma 函数的推广
Gamma 函数可以推广到复数域,并且除了 $x = 0, -1, -2, -3, \dots$ 这些点(它们是极点),在整个复平面都是解析的。这种推广在复分析和特殊函数理论中非常重要。
总结
- Gamma 函数是阶乘的推广,并满足 $\Gamma(n) = (n-1)!$。
- 它具有递推关系 $\Gamma(x+1) = x\Gamma(x)$。
- 重要特殊值:$\Gamma(1) = 1$,$\Gamma(1/2) = \sqrt{\pi}$。
- 反射公式 $\Gamma(x)\Gamma(1-x) = \frac{\pi}{\sin(\pi x)}$。
- 斯特林公式可用于近似计算 Gamma 函数。
14. Beta函数
1. Beta 函数的定义
Beta 函数 $B(x, y)$ 是一个重要的特殊函数,定义为:
$$
B(x, y) = \int_0^1 t^{x-1} (1 - t)^{y-1} dt, \quad x > 0, \ y > 0
$$
它在许多数学分析、概率论和物理学问题中有广泛的应用。
2. Beta 函数与 Gamma 函数的关系
Beta 函数可以通过 Gamma 函数表示,其最重要的性质是:
$$
B(x, y) = \frac{\Gamma(x) \Gamma(y)}{\Gamma(x + y)}
$$
其中 $ \Gamma(x) $ 是 Gamma 函数。这一性质表明 Beta 函数可以看作 Gamma 函数的比值。
3. Beta 函数的性质
(1) 对称性
Beta 函数满足交换律,即:
$$
B(x, y) = B(y, x)
$$
这可以直接从定义式中 $t \to (1-t)$ 的变量代换推导出。
(2) 递推关系
Beta 函数的递推关系类似于 Gamma 函数:
$$
B(x+1, y) = \frac{x}{x + y} B(x, y)
$$
$$
B(x, y+1) = \frac{y}{x + y} B(x, y)
$$
(3) 结合积分计算
在计算某些积分时,Beta 函数提供了有用的公式:
$$
\int_0^\infty \frac{t^{x-1}}{(1+t)^{x+y}} dt = B(x, y)
$$
这个积分在概率论和随机变量分析中常见。
(4) 通过 Gamma 函数计算特殊值
利用 $\Gamma(x)$ 的性质,可以计算 $B(x, y)$ 的一些具体值。例如,当 $x = y = 1/2$ 时:
$$
B\left(\frac{1}{2}, \frac{1}{2}\right) = \frac{\Gamma(1/2) \Gamma(1/2)}{\Gamma(1)}
$$
由于 $\Gamma(1/2) = \sqrt{\pi}$,且 $\Gamma(1) = 1$,所以:
$$
B\left(\frac{1}{2}, \frac{1}{2}\right) = \frac{\pi}{\Gamma(1)} = \pi
$$
4. Beta 函数的应用
(1) 在概率论中的应用
Beta 分布是一个常见的概率分布,其概率密度函数(PDF)为:
$$
f(x; \alpha, \beta) = \frac{x^{\alpha - 1} (1 - x)^{\beta - 1}}{B(\alpha, \beta)}, \quad 0 < x < 1
$$
Beta 分布在贝叶斯统计、顺序检验等领域有广泛应用。
(2) 在组合数学中的应用
Beta 函数可以用于计算某些组合数公式,例如:
$$
B(n, m) = \frac{(n-1)! (m-1)!}{(n+m-1)!}
$$
这在组合分析和统计物理中有所应用。
(3) 在积分计算中的应用
Beta 函数常用于计算涉及二项式的积分,例如:
$$
\int_0^1 x^{m-1} (1 - x)^{n-1} dx = B(m, n)
$$
这在数学分析和应用数学中经常出现。
总结
- Beta 函数的定义为 $B(x, y) = \int_0^1 t^{x-1} (1 - t)^{y-1} dt$,适用于 $x, y > 0$。
- Beta 函数与 Gamma 函数的关系:$B(x, y) = \frac{\Gamma(x) \Gamma(y)}{\Gamma(x + y)}$。
- 具有对称性:$B(x, y) = B(y, x)$。
- 递推关系:$B(x+1, y) = \frac{x}{x + y} B(x, y)$。
- 重要特殊值:$B(1/2, 1/2) = \pi$。
- 在概率论(Beta 分布)、组合数学和积分计算中有广泛应用。
15. 向量乘法相关
15.1 向量点乘
向量点乘(内积)是两个向量相乘的一种方式,其结果是一个标量,反映了两个向量在同一方向上的相似程度。它在几何、物理和计算机科学中具有重要应用,如计算投影、夹角以及能量计算等。
给定两个 $n$ 维向量 $\mathbf{A} = (a_1, a_2, \dots, a_n)$ 和 $\mathbf{B} = (b_1, b_2, \dots, b_n)$,它们的点乘定义为:
$$
\mathbf{A} \cdot \mathbf{B} = \sum_{i=1}^{n} a_i b_i
$$
在三维空间中,点乘可以表示为:
$$
\mathbf{A} \cdot \mathbf{B} = a_x b_x + a_y b_y + a_z b_z
$$
重要公式
- 代数定义(坐标形式):
$$
\mathbf{A} \cdot \mathbf{B} = \sum_{i=1}^{n} a_i b_i
$$
- 几何定义(角度关系):
$$
\mathbf{A} \cdot \mathbf{B} = |\mathbf{A}| |\mathbf{B}| \cos \theta
$$
其中 $|\mathbf{A}|$ 和 $|\mathbf{B}|$ 分别是 $\mathbf{A}$ 和 $\mathbf{B}$ 的模,$\theta$ 是它们之间的夹角。
- 单位向量的点乘:
$$
\mathbf{i} \cdot \mathbf{i} = \mathbf{j} \cdot \mathbf{j} = \mathbf{k} \cdot \mathbf{k} = 1
$$
$$
\mathbf{i} \cdot \mathbf{j} = \mathbf{j} \cdot \mathbf{k} = \mathbf{k} \cdot \mathbf{i} = 0
$$
投影公式:
向量 $\mathbf{A}$ 在向量 $\mathbf{B}$ 方向上的投影:
$$
\text{proj}_{\mathbf{B}} \mathbf{A} = \frac{\mathbf{A} \cdot \mathbf{B}}{|\mathbf{B}|}
$$正交判别(向量垂直的条件):
若 $\mathbf{A} \cdot \mathbf{B} = 0$,则 $\mathbf{A}$ 与 $\mathbf{B}$ 垂直。
15.2 向量叉乘
相关概念
向量叉乘(外积)是另一种向量乘法,它适用于三维向量,并且结果是一个新的向量,而不是标量。它在物理(如力矩、磁场计算)和计算机图形学(如法向量计算)中有广泛应用。
给定两个三维向量 $\mathbf{A} = (a_x, a_y, a_z)$ 和 $\mathbf{B} = (b_x, b_y, b_z)$,它们的叉乘 $\mathbf{A} \times \mathbf{B}$ 计算如下:
$$
\mathbf{A} \times \mathbf{B} =
\begin{vmatrix}
\mathbf{i} & \mathbf{j} & \mathbf{k} \\
a_x & a_y & a_z \\
b_x & b_y & b_z
\end{vmatrix}
$$
展开行列式得:
$$
\mathbf{A} \times \mathbf{B} =
\begin{bmatrix}
a_y b_z - a_z b_y \\
a_z b_x - a_x b_z \\
a_x b_y - a_y b_x
\end{bmatrix}
$$
重要公式
- 代数定义(坐标形式):
$$
\mathbf{A} \times \mathbf{B} =
\begin{bmatrix}
a_y b_z - a_z b_y \\
a_z b_x - a_x b_z \\
a_x b_y - a_y b_x
\end{bmatrix}
$$
- 几何定义(模长):
叉乘的模长为:
$$
|\mathbf{A} \times \mathbf{B}| = |\mathbf{A}| |\mathbf{B}| \sin \theta
$$
其中 $\theta$ 是 $\mathbf{A}$ 和 $\mathbf{B}$ 之间的夹角。
- $|\mathbf{A}| |\mathbf{B}| \sin \theta$ 表示 $\mathbf{A}$ 和 $\mathbf{B}$为邻边的平行四边形的面积
方向判定(右手定则):
叉乘的方向由右手定则确定:右手四指从 $\mathbf{A}$ 指向 $\mathbf{B}$,大拇指的方向就是 $\mathbf{A} \times \mathbf{B}$ 的方向。单位向量的叉乘:
$$
\mathbf{i} \times \mathbf{j} = \mathbf{k}, \quad
\mathbf{j} \times \mathbf{k} = \mathbf{i}, \quad
\mathbf{k} \times \mathbf{i} = \mathbf{j}
$$
$$
\mathbf{j} \times \mathbf{i} = -\mathbf{k}, \quad
\mathbf{k} \times \mathbf{j} = -\mathbf{i}, \quad
\mathbf{i} \times \mathbf{k} = -\mathbf{j}
$$
平行向量的叉乘(零向量):
若 $\mathbf{A} \parallel \mathbf{B}$,则 $\mathbf{A} \times \mathbf{B} = \mathbf{0}$。
混合积(体积计算):
三个向量 $\mathbf{A}, \mathbf{B}, \mathbf{C}$ 组成的平行六面体体积可通过混合积计算:
$$
V = |\mathbf{A} \cdot (\mathbf{B} \times \mathbf{C})|
$$
15.3 总结
向量点乘:
- 计算公式:$\mathbf{A} \cdot \mathbf{B} = |\mathbf{A}| |\mathbf{B}| \cos \theta$。
- 结果是一个标量,表示两个向量的相似程度。
- 用于计算投影、角度、正交性等。
向量叉乘:
- 计算公式:$\mathbf{A} \times \mathbf{B} = (a_y b_z - a_z b_y, a_z b_x - a_x b_z, a_x b_y - a_y b_x)$。
- 结果是一个向量,垂直于原向量所在平面。
- 用于计算法向量、角动量、力矩等。
16. 三维空间的平面方程
在三维空间中,平面是由一点和一个法向量唯一确定的。平面方程可以有不同的表示方式,包括一般式、点法式和截距式,每种形式在不同的应用场景下有不同的优势。
16.1. 一般式
平面的一般式是最常见的平面方程形式,它描述了平面上的所有点满足的一个线性方程。
$$
Ax + By + Cz + D = 0
$$
其中:
- $(A, B, C)$ 是平面的法向量,表示平面垂直于该方向。
- $D$ 是常数项,决定了平面与坐标轴的相对位置。
- 任意在该平面上的点 $(x, y, z)$ 都满足该方程。
特点
- 通用性强,适用于解析几何和计算交点问题。
- 法向量 $(A, B, C)$ 直观地表示平面的方向。
- 通过已知三点 $(x_1, y_1, z_1)$, $(x_2, y_2, z_2)$, $(x_3, y_3, z_3)$,可求出平面方程:
$$
\begin{vmatrix}
x - x_1 & y - y_1 & z - z_1 \\
x_2 - x_1 & y_2 - y_1 & z_2 - z_1 \\
x_3 - x_1 & y_3 - y_1 & z_3 - z_1
\end{vmatrix} = 0
$$
16.2. 点法式
平面的点法式(点法向量式)方程由平面上一点和法向量来唯一确定。
$$
A(x - x_0) + B(y - y_0) + C(z - z_0) = 0
$$
其中:
- $(x_0, y_0, z_0)$ 是已知的平面上一点。
- $(A, B, C)$ 是平面的法向量,表示平面的方向。
特点
- 形式直观,直接体现了平面经过某一点,并由法向量决定方向。
- 适用于已知一点和法向量的情况,如物理中的力场计算。
- 适用于计算点到平面的距离:
$$
d = \frac{|Ax_1 + By_1 + Cz_1 + D|}{\sqrt{A^2 + B^2 + C^2}}
$$
其中 $(x_1, y_1, z_1)$ 是平外一点。
16.3. 截距式
截距式描述了平面与坐标轴的交点,适用于平面与坐标轴都有交点的情况。
$$
\frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1
$$
其中:
- $a, b, c$ 分别是平面在 $x$、$y$ 和 $z$ 轴上的截距,即平面与坐标轴的交点 $(a, 0, 0)$,$(0, b, 0)$,$(0, 0, c)$。
特点
- 适用于平面与三坐标轴均有交点的情况。
- 若平面平行于某坐标轴,则该坐标轴方向上的截距不存在,不能使用该公式。
- 形式简洁,适用于几何分析。
16.4. 总结
一般式:
- 公式:$Ax + By + Cz + D = 0$。
- 适用于解析几何计算,法向量 $(A, B, C)$ 直观表示平面方向。
点法式(点法向量式):
- 公式:$A(x - x_0) + B(y - y_0) + C(z - z_0) = 0$。
- 适用于已知一点和法向量的情况,可用于计算点到平面的距离。
截距式:
- 公式:$\frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1$。
- 适用于平面与三坐标轴都有交点的情况,形式直观。
三维空间的平面方程在物理、计算机图形学、工程计算等领域中有广泛应用!
17. 三维空间的直线方程
在三维空间中,直线不再仅由一个斜率描述,而是需要用方向向量或参数来表示。常见的三维直线方程形式包括一般式、点法式和截距式。
17.1. 一般式
一般式是三维直线的隐式方程,它由两个平面的交集表示。由于两个平面唯一确定一条直线,因此可以用两个线性方程组来描述三维直线。
若直线是两个平面方程的交线,则可以表示为:
$$
A_1x + B_1y + C_1z + D_1 = 0
$$
$$
A_2x + B_2y + C_2z + D_2 = 0
$$
其中,$(A_1, B_1, C_1)$ 和 $(A_2, B_2, C_2)$ 分别是两个平面的法向量,两个方程联立可以唯一确定直线。
特点
- 适用于解析几何中的直线求交问题。
- 通过解方程组求出直线上的点。
- 适用于与平面方程配合使用,但不够直观。
17.2. 点法式
点法式(参数方程)使用直线上一点和一个方向向量来唯一确定直线。方向向量 $\mathbf{d} = (l, m, n)$ 表示直线的方向,而直线上一点 $P_0(x_0, y_0, z_0)$ 用于定位。
重要公式
直线的点法式方程(参数方程):
$$
x = x_0 + lt
$$
$$
y = y_0 + mt
$$
$$
z = z_0 + nt
$$
其中:
- $P_0(x_0, y_0, z_0)$ 是直线上已知的一点。
- 方向向量 $\mathbf{d} = (l, m, n)$ 决定了直线的方向。
- $t$ 是参数,表示不同的点。
特点
- 直观且易于计算,适用于物理和工程中的轨迹问题。
- 可以直接用于计算直线与平面的交点(代入平面方程)。
- 方向向量不能为零向量,否则无法确定方向。
17.3. 截距式
截距式描述了直线在各坐标轴上的截距。当直线与坐标轴有明确交点时,可以使用这种形式。
三维空间中的直线截距式可以表示为:
$$
\frac{x}{a} = \frac{y}{b} = \frac{z}{c}
$$
其中:
- $a, b, c$ 为直线在 $x$、$y$、$z$ 轴上的截距。
- 若直线经过原点,则该式不适用(因分母不能为零)。
特点
- 适用于直线与三坐标轴都有交点的情况。
- 形式简洁,直观显示直线与坐标轴的关系。
- 不能用于方向向量平行于某坐标轴的情况。
17.4.总结
一般式:
- 由两个平面方程的交集表示:
$A_1x + B_1y + C_1z + D_1 = 0$,$A_2x + B_2y + C_2z + D_2 = 0$。 - 适用于解析几何问题,如直线交点计算。
- 由两个平面方程的交集表示:
点法式(参数方程):
- 直线上一点 $P_0(x_0, y_0, z_0)$ 和方向向量 $\mathbf{d} = (l, m, n)$。
- 公式:
$x = x_0 + lt$,
$y = y_0 + mt$,
$z = z_0 + nt$。 - 适用于运动轨迹和计算交点问题。
截距式:
- 适用于直线与坐标轴有截距的情况。
- 公式:$\frac{x}{a} = \frac{y}{b} = \frac{z}{c}$。
- 不能用于直线经过原点的情况。
18. 平面与平面的关系
在三维空间中,两个平面可以是平行的、相交的或重合的。我们可以通过法向量的关系来判断它们的几何关系,并计算它们的夹角。
18.1. 如何判断两个平面平行
两个平面平行,当且仅当它们的法向量共线,即法向量成比例。
设两个平面方程为:
$$
A_1x + B_1y + C_1z + D_1 = 0
$$
$$
A_2x + B_2y + C_2z + D_2 = 0
$$
若它们的法向量 $\mathbf{n_1} = (A_1, B_1, C_1)$ 和 $\mathbf{n_2} = (A_2, B_2, C_2)$ 成比例,即存在非零常数 $k$ 使得:
$$
(A_2, B_2, C_2) = k (A_1, B_1, C_1)
$$
则两个平面平行。
18.2. 如何判断两个平面垂直
两个平面垂直,当且仅当它们的法向量垂直,即法向量的点积为零。
$$
\mathbf{n_1} \cdot \mathbf{n_2} = A_1 A_2 + B_1 B_2 + C_1 C_2 = 0
$$
若满足此条件,则两个平面垂直。
18.3. 如何计算两个平面的夹角
两个平面的夹角等于它们法向量的夹角,由点积公式计算。
设两个法向量 $\mathbf{n_1}$ 和 $\mathbf{n_2}$ 的夹角为 $\theta$,则:
$$
\cos\theta = \frac{\mathbf{n_1} \cdot \mathbf{n_2}}{|\mathbf{n_1}| |\mathbf{n_2}|}
$$
其中:
- $|\mathbf{n_1}| = \sqrt{A_1^2 + B_1^2 + C_1^2}$ 是 $\mathbf{n_1}$ 的模长。
- $|\mathbf{n_2}| = \sqrt{A_2^2 + B_2^2 + C_2^2}$ 是 $\mathbf{n_2}$ 的模长。
19. 直线与直线的关系
在三维空间中,两个直线可以是平行的、相交的或异面的。我们可以通过它们的方向向量来判断它们的关系,并计算夹角。
19.1. 如何判断两条直线平行
两条直线平行,当且仅当它们的方向向量共线,即方向向量成比例。
设两条直线的方向向量分别为 $\mathbf{d_1} = (l_1, m_1, n_1)$ 和 $\mathbf{d_2} = (l_2, m_2, n_2)$,若存在非零常数 $k$ 使得:
$$
(l_2, m_2, n_2) = k (l_1, m_1, n_1)
$$
则两条直线平行。
19.2. 如何判断两条直线垂直
两条直线垂直,当且仅当它们的方向向量垂直,即方向向量的点积为零。
$$
\mathbf{d_1} \cdot \mathbf{d_2} = l_1 l_2 + m_1 m_2 + n_1 n_2 = 0
$$
若满足此条件,则两条直线垂直。
19.3. 如何计算两条直线的夹角
两条直线的夹角等于它们方向向量的夹角,由点积公式计算。
设两条直线的方向向量 $\mathbf{d_1}$ 和 $\mathbf{d_2}$ 夹角为 $\theta$,则:
$$
\cos\theta = \frac{\mathbf{d_1} \cdot \mathbf{d_2}}{|\mathbf{d_1}| |\mathbf{d_2}|}
$$
其中:
- $|\mathbf{d_1}| = \sqrt{l_1^2 + m_1^2 + n_1^2}$ 是 $\mathbf{d_1}$ 的模长。
- $|\mathbf{d_2}| = \sqrt{l_2^2 + m_2^2 + n_2^2}$ 是 $\mathbf{d_2}$ 的模长。
20. 直线与平面的关系
直线与平面可能是相交的、平行的或在平面内。我们可以通过方向向量和法向量的关系来判断它们的几何关系,并计算夹角。
20.1. 如何判断直线与平面垂直
直线与平面垂直,当且仅当直线的方向向量与平面的法向量平行,即方向向量成比例。
设直线的方向向量为 $\mathbf{d} = (l, m, n)$,平面的法向量为 $\mathbf{n} = (A, B, C)$,若存在非零常数 $k$ 使得:
$$
(A, B, C) = k (l, m, n)
$$
则直线与平面垂直。
20.2. 如何判断直线在平面上
直线在平面上,当且仅当直线的方向向量与平面的法向量垂直,且直线上一点满足平面方程。
重要公式
(1) 直线的方向向量 $\mathbf{d} = (l, m, n)$ 满足:
$$
\mathbf{d} \cdot \mathbf{n} = lA + mB + nC = 0
$$
(2) 直线上一点 $(x_0, y_0, z_0)$ 代入平面方程:
$$
A x_0 + B y_0 + C z_0 + D = 0
$$
若两者均满足,则直线在平面上。
20.3. 如何求直线和平面的夹角
直线与平面的夹角是指直线方向向量与平面法向量的夹角的补角。
设直线方向向量为 $\mathbf{d} = (l, m, n)$,平面法向量为 $\mathbf{n} = (A, B, C)$,夹角 $\theta$ 满足:
$$
\sin\theta = \frac{|\mathbf{d} \cdot \mathbf{n}|}{|\mathbf{d}| |\mathbf{n}|}
$$
其中 $\theta$ 为直线与平面的夹角(取锐角)。
21. 偏导数(partial derivative)
偏导数是多元函数在某一方向上的变化率,描述了函数对某个特定变量的变化率,而其他变量保持不变。
21.1. 偏导数的几何意义
在单变量微积分中,导数表示曲线在某点的切线斜率,而在多元函数中,偏导数描述函数在某个方向上的变化率。
设 $z = f(x, y)$ 是一个二元函数,其偏导数的几何意义为:
- $\frac{\partial f}{\partial x}$:表示在 $y$ 固定时,函数沿 $x$ 方向的变化率,对应于曲面 $z = f(x, y)$ 在 $x$ 方向的切线斜率。
- $\frac{\partial f}{\partial y}$:表示在 $x$ 固定时,函数沿 $y$ 方向的变化率,对应于曲面 $z = f(x, y)$ 在 $y$ 方向的切线斜率。
偏导数的定义:
$$
\frac{\partial f}{\partial x} = \lim\limits_{h \to 0} \frac{f(x+h, y) - f(x, y)}{h}
$$
$$
\frac{\partial f}{\partial y} = \lim\limits_{h \to 0} \frac{f(x, y+h) - f(x, y)}{h}
$$
若 $f(x, y)$ 可微,则其全微分为:
$$
dz = \frac{\partial f}{\partial x} dx + \frac{\partial f}{\partial y} dy
$$
表示函数在 $x$ 和 $y$ 方向上的变化综合作用。
21.2. 多元函数求偏导数
在求偏导数时,只对指定的变量求导,将其他变量视为常数。例如:
- 求 $\frac{\partial f}{\partial x}$ 时,$y$ 视为常数;
- 求 $\frac{\partial f}{\partial y}$ 时,$x$ 视为常数。
设 $f(x, y) = x^2y + e^x \sin y$,则:
$$
\frac{\partial f}{\partial x} = 2xy + e^x \sin y
$$
$$
\frac{\partial f}{\partial y} = x^2 + e^x \cos y
$$
若 $f(x, y, z) = x^2 y + yz^3 + \ln z$,则:
$$
\frac{\partial f}{\partial x} = 2xy
$$
$$
\frac{\partial f}{\partial y} = x^2 + z^3
$$
$$
\frac{\partial f}{\partial z} = 3yz^2 + \frac{1}{z}
$$
21.3. 偏导数的链式法则
当 $z = f(x, y)$ 且 $x, y$ 由另一个变量 $t$ 变化时,可以使用链式法则计算 $z$ 对 $t$ 的变化率。
重要公式
(1) 单参数情况
若 $x = x(t)$,$y = y(t)$,则:
$$
\frac{dz}{dt} = \frac{\partial f}{\partial x} \frac{dx}{dt} + \frac{\partial f}{\partial y} \frac{dy}{dt}
$$
(2) 多参数情况
若 $z = f(x, y)$,其中 $x = x(u, v)$,$y = y(u, v)$,则:
$$
\frac{\partial z}{\partial u} = \frac{\partial f}{\partial x} \frac{\partial x}{\partial u} + \frac{\partial f}{\partial y} \frac{\partial y}{\partial u}
$$
$$
\frac{\partial z}{\partial v} = \frac{\partial f}{\partial x} \frac{\partial x}{\partial v} + \frac{\partial f}{\partial y} \frac{\partial y}{\partial v}
$$
示例
设 $z = x^2 + xy$,其中 $x = t^2, y = e^t$,则:
$$
\frac{\partial f}{\partial x} = 2x + y, \quad \frac{\partial f}{\partial y} = x
$$
$$
\frac{dx}{dt} = 2t, \quad \frac{dy}{dt} = e^t
$$
则:
$$
\frac{dz}{dt} = (2x + y) \cdot 2t + x \cdot e^t
$$
代入 $x = t^2, y = e^t$,得:
$$
\frac{dz}{dt} = (2t^2 + e^t) \cdot 2t + t^2 e^t
$$
总结
- 偏导数描述多元函数在某个方向上的变化率,几何上表示曲面的切线斜率。
- 求偏导时,仅对指定变量求导,其余变量视为常数。
- 偏导数的链式法则用于计算复合函数的变化率,在多元微积分和物理中广泛应用。
22. 二元函数的极值判断
在二元函数 $f(x, y)$ 中,极值点是使函数达到局部最大值或最小值的点。我们可以通过 二阶偏导数判别法(即 $\Delta$ 方法)来判断极值。
22.1. 关键概念
设 $f(x, y)$ 是二元可微函数,若在点 $(x_0, y_0)$ 处有:
$$
\frac{\partial f}{\partial x} = 0, \quad \frac{\partial f}{\partial y} = 0
$$
则称 $(x_0, y_0)$ 为驻点(临界点),可能是极大值、极小值或鞍点。
为了进一步判断驻点的性质,需要计算 二阶偏导数判别式:
$$
\Delta = f_{xx} f_{yy} - (f_{xy})^2
$$
其中:
- $f_{xx} = \frac{\partial^2 f}{\partial x^2}$ 是 $x$ 方向的二阶偏导数。
- $f_{yy} = \frac{\partial^2 f}{\partial y^2}$ 是 $y$ 方向的二阶偏导数。
- $f_{xy} = \frac{\partial^2 f}{\partial x \partial y}$ 是混合偏导数。
22.2. 极值判断方法($\Delta$ 方法)
- 若 $\Delta > 0$ 且 $f_{xx} > 0$,则 $(x_0, y_0)$ 为局部极小值。
- 若 $\Delta > 0$ 且 $f_{xx} < 0$,则 $(x_0, y_0)$ 为局部极大值。
- 若 $\Delta < 0$,则 $(x_0, y_0)$ 为鞍点(既不是极大值也不是极小值)。
- 若 $\Delta = 0$,无法判断,需要进一步分析。
22.3. 重要公式
一阶条件(求驻点):
$$
\frac{\partial f}{\partial x} = 0, \quad \frac{\partial f}{\partial y} = 0
$$二阶判别式(判断极值):
$$
\Delta = f_{xx} f_{yy} - (f_{xy})^2
$$
根据 $\Delta$ 的取值判断极值类型。
22.4. 示例
例 1:判断函数 $f(x, y) = x^3 + y^3 - 3xy$ 的极值*
第一步:求驻点
计算一阶偏导数:
$$
f_x = 3x^2 - 3y = 0
$$
$$
f_y = 3y^2 - 3x = 0
$$
解方程组:
$$
\begin{cases}
3x^2 - 3y = 0 \quad \Rightarrow \quad y = x^2 \\
3y^2 - 3x = 0 \quad \Rightarrow \quad x = y^2
\end{cases}
$$
代入 $y = x^2$ 到 $x = y^2$:
$$
x = (x^2)^2 = x^4
$$
即:
$$
x^4 - x = 0 \quad \Rightarrow \quad x(x^3 - 1) = 0
$$
解得:
$$
x = 0, \quad x = 1, \quad x = -1
$$
代入 $y = x^2$:
$$
(0,0), \quad (1,1), \quad (-1,1)
$$
第二步:计算二阶偏导数
$$
f_{xx} = 6x, \quad f_{yy} = 6y, \quad f_{xy} = -3
$$
计算 $\Delta$:
$$
\Delta = f_{xx} f_{yy} - (f_{xy})^2 = (6x)(6y) - (-3)^2
$$
第三步:判断极值
点 $(0,0)$:
$$
\Delta = (6 \cdot 0)(6 \cdot 0) - (-3)^2 = -9 < 0
$$由于 $\Delta < 0$,$(0,0)$ 是鞍点。
点 $(1,1)$:
$$
\Delta = (6 \cdot 1)(6 \cdot 1) - (-3)^2 = 36 - 9 = 27 > 0
$$由于 $\Delta > 0$ 且 $f_{xx} = 6 > 0$,$(1,1)$ 是局部极小值。
点 $(-1,1)$:
$$
\Delta = (6 \cdot (-1))(6 \cdot 1) - (-3)^2 = -36 - 9 = -45 < 0
$$由于 $\Delta < 0$,$(-1,1)$ 也是鞍点。
总结
- 求驻点:令 $\frac{\partial f}{\partial x} = 0, \frac{\partial f}{\partial y} = 0$,解方程组。
- 计算二阶偏导数:$f_{xx}, f_{yy}, f_{xy}$。
- 计算 $\Delta = f_{xx} f_{yy} - (f_{xy})^2$ 并判断极值:
- 若 $\Delta > 0$ 且 $f_{xx} > 0$,则是局部极小值。
- 若 $\Delta > 0$ 且 $f_{xx} < 0$,则是局部极大值。
- 若 $\Delta < 0$,则是鞍点。
- 若 $\Delta = 0$,需进一步分析。
23. 梯度(Gradient)
在微积分中,梯度(Gradient)描述的是一个多元函数在某一点处的最大变化率及其方向。梯度是一个向量,表示函数在该点的最陡上升方向。
设 $f(x,y)$ 是一个二元函数,其梯度记为 $\nabla f$(nabla 读作“纳布拉”),定义如下:
$$
\nabla f = \left( \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y} \right)
$$
若 $f$ 是三元函数 $f(x,y,z)$,其梯度则为:
$$
\nabla f = \left( \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}, \frac{\partial f}{\partial z} \right)
$$
梯度的几何意义:
梯度向量 $\nabla f$ 指向函数值增长最快的方向,其模长 $|\nabla f|$ 代表该方向上的最大变化率。
- 若 $\nabla f = 0$,则函数在该点处达到极值或是一个平稳点。
- 梯度的方向与等高线(即 $f(x,y) = c$ 的曲线)垂直。
梯度的应用:
最速上升方向:梯度的方向是函数增长最快的方向。
法向量:在某点 $(x_0, y_0)$ 处,$\nabla f(x_0, y_0)$ 代表等高线 $f(x,y) = c$ 的法向量。
方向导数:沿任意方向 $\mathbf{v} = (v_x, v_y)$ 的变化率可由梯度计算:
$$
D_{\mathbf{v}} f = \nabla f \cdot \mathbf{v} = \frac{\partial f}{\partial x} v_x + \frac{\partial f}{\partial y} v_y
$$
示例
设 $f(x,y) = x^2 + y^2$,计算其梯度:
$$
\nabla f = \left( \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y} \right) = (2x, 2y)
$$
在点 $(1,2)$ 处:
$$
\nabla f(1,2) = (2,4)
$$
表示该点处函数增长最快的方向为 $(2,4)$,即沿着该方向移动时 $f(x,y)$ 变化最快。
总结
- 梯度的定义:$\nabla f = (\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}, \cdots)$
- 梯度的几何意义:指向函数值增长最快的方向,且与等高线垂直。
- 梯度的应用:
- 确定最速上升方向
- 计算方向导数
- 作为等高线的法向量
24. 散度(Divergence)
在微积分中,散度(Divergence) 描述的是一个向量场在某一点的“发散”或“汇聚”程度。它衡量的是向量场的体积膨胀或收缩趋势。
设 $\mathbf{F}$ 是一个三维向量场:
$$
\mathbf{F} = (P, Q, R)
$$
其中 $P, Q, R$ 分别是 $x, y, z$ 的函数,则散度(记作 $\nabla \cdot \mathbf{F}$)定义为:
$$
\nabla \cdot \mathbf{F} = \frac{\partial P}{\partial x} + \frac{\partial Q}{\partial y} + \frac{\partial R}{\partial z}
$$
若 $\mathbf{F}$ 是二维向量场 $\mathbf{F} = (P, Q)$,则散度为:
$$
\nabla \cdot \mathbf{F} = \frac{\partial P}{\partial x} + \frac{\partial Q}{\partial y}
$$
24.1. 散度的物理意义
- 正散度($\nabla \cdot \mathbf{F} > 0$):向量场在该点处“发散”,即周围有“源”。
- 负散度($\nabla \cdot \mathbf{F} < 0$):向量场在该点处“汇聚”,即周围有“汇”。
- 零散度($\nabla \cdot \mathbf{F} = 0$):表示该点附近没有净体积膨胀或收缩。
24.2. 示例
设向量场:
$$
\mathbf{F} = (x^2, y^2, z^2)
$$
计算散度:
$$
\nabla \cdot \mathbf{F} = \frac{\partial}{\partial x} (x^2) + \frac{\partial}{\partial y} (y^2) + \frac{\partial}{\partial z} (z^2)
$$
$$
= 2x + 2y + 2z
$$
在点 $(1,1,1)$ 处:
$$
\nabla \cdot \mathbf{F} = 2(1) + 2(1) + 2(1) = 6
$$
表示该点处的向量场有较强的发散趋势。
24.3 总结
- 散度的定义:
$$
\nabla \cdot \mathbf{F} = \frac{\partial P}{\partial x} + \frac{\partial Q}{\partial y} + \frac{\partial R}{\partial z}
$$ - 散度的几何意义:
- $\nabla \cdot \mathbf{F} > 0$:源(向外发散)。
- $\nabla \cdot \mathbf{F} < 0$:汇(向内收缩)。
- $\nabla \cdot \mathbf{F} = 0$:无散场。
- 散度的应用:
- 流体力学:表示流体的局部膨胀或压缩。
- 电磁学:高斯定理用于描述电场的散度。
- 向量场分析:判断向量场是否为无散场。
25. 旋度(Curl)
在微积分中,旋度(Curl)描述的是一个向量场在某一点的旋转或绕流程度。它衡量的是向量场的局部旋转趋势,即围绕某点的小范围流体是否存在旋转效应。
设 $\mathbf{F}$ 是三维向量场:
$$
\mathbf{F} = (P, Q, R)
$$
其中 $P, Q, R$ 分别是 $x, y, z$ 的函数,则旋度(记作 $\nabla \times \mathbf{F}$)定义为:
$$
\nabla \times \mathbf{F} =
\begin{vmatrix}
\mathbf{i} & \mathbf{j} & \mathbf{k} \\
\frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\
P & Q & R
\end{vmatrix}
$$
展开行列式后:
$$
\nabla \times \mathbf{F} =
\left(
\frac{\partial R}{\partial y} - \frac{\partial Q}{\partial z},
\frac{\partial P}{\partial z} - \frac{\partial R}{\partial x},
\frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y}
\right)
$$
若 $\mathbf{F}$ 是二维向量场 $\mathbf{F} = (P, Q)$,则旋度可以写为:
$$
\nabla \times \mathbf{F} = \frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y}
$$
此时旋度是一个标量,而在三维中旋度是一个向量。
25.1. 旋度的几何意义
- $\nabla \times \mathbf{F} \neq 0$:向量场在该点附近存在旋转趋势,表示局部旋转效应。
- $\nabla \times \mathbf{F} = 0$:向量场在该点附近无旋转趋势,即场是无旋场。
旋度的方向给出流体旋转的轴向方向,而旋度的模长表示旋转的强度。
25.2. 示例
设向量场:
$$
\mathbf{F} = (y, -x, 0)
$$
计算旋度:
$$
\nabla \times \mathbf{F} =
\begin{vmatrix}
\mathbf{i} & \mathbf{j} & \mathbf{k} \\
\frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\
y & -x & 0
\end{vmatrix}
$$
$$
= \left( \frac{\partial 0}{\partial y} - \frac{\partial (-x)}{\partial z}, \frac{\partial y}{\partial z} - \frac{\partial 0}{\partial x}, \frac{\partial (-x)}{\partial x} - \frac{\partial y}{\partial y} \right)
$$
$$
= (0 - 0, 0 - 0, -1 - 1) = (0,0,-2)
$$
表示该向量场在 $z$ 方向上有一个逆时针旋转的趋势。
25.3. 总结
旋度的定义:
$$
\nabla \times \mathbf{F} =
\begin{vmatrix}
\mathbf{i} & \mathbf{j} & \mathbf{k} \\
\frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\
P & Q & R
\end{vmatrix}
$$旋度的几何意义:
- $\nabla \times \mathbf{F} \neq 0$:表示向量场具有旋转趋势。
- $\nabla \times \mathbf{F} = 0$:表示无旋场。
旋度的应用:
- 流体力学:判断流体是否有旋转效应。
- 电磁学:麦克斯韦方程描述电磁场的旋度。
- 向量场分析:判断向量场是否可由势函数表示。
26. 雅可比行列式(Jacobian Determinant)
在微积分和向量分析中,雅可比行列式(Jacobian Determinant) 描述了多元函数的局部伸缩变换程度。它用于坐标变换、隐函数定理和多重积分的变量代换。
设一个向量值函数:
$$
\mathbf{F}(x_1, x_2, \dots, x_n) = (f_1, f_2, \dots, f_n)
$$
其中,每个 $f_i$ 是 $n$ 个变量的函数,则 雅可比矩阵(Jacobian Matrix) 定义为:
$$
J =
\begin{bmatrix}
\frac{\partial f_1}{\partial x_1} & \frac{\partial f_1}{\partial x_2} & \dots & \frac{\partial f_1}{\partial x_n} \\
\frac{\partial f_2}{\partial x_1} & \frac{\partial f_2}{\partial x_2} & \dots & \frac{\partial f_2}{\partial x_n} \\
\vdots & \vdots & \ddots & \vdots \\
\frac{\partial f_n}{\partial x_1} & \frac{\partial f_n}{\partial x_2} & \dots & \frac{\partial f_n}{\partial x_n}
\end{bmatrix}
$$
雅可比行列式(Jacobian Determinant)定义为:
$$
\det(J) = \begin{vmatrix}
\frac{\partial f_1}{\partial x_1} & \frac{\partial f_1}{\partial x_2} & \dots & \frac{\partial f_1}{\partial x_n} \\
\frac{\partial f_2}{\partial x_1} & \frac{\partial f_2}{\partial x_2} & \dots & \frac{\partial f_2}{\partial x_n} \\
\vdots & \vdots & \ddots & \vdots \\
\frac{\partial f_n}{\partial x_1} & \frac{\partial f_n}{\partial x_2} & \dots & \frac{\partial f_n}{\partial x_n}
\end{vmatrix}
$$
26.1. 雅可比行列式的几何意义
- $\det(J) > 0$:局部变换保持方向(不翻转)。
- $\det(J) < 0$:局部变换导致翻转(如镜像变换)。
- $\det(J) = 0$:变换在该点处不可逆(例如折叠或压缩成低维结构)。
雅可比行列式的绝对值 $|\det(J)|$ 表示变换前后体积的局部伸缩比例。在变量替换的积分计算中,它用于调整体积元素。
26.2. 示例
设二维坐标变换:
$$
x = r\cos\theta, \quad y = r\sin\theta
$$
$$
\det(J) =
\begin{vmatrix}
\cos\theta & -r\sin\theta \\
\sin\theta & r\cos\theta
\end{vmatrix}
= r(\cos^2\theta + \sin^2\theta) = r
$$
在极坐标积分中,$dx,dy$ 需要乘以 $|\det(J)| = r$,即:
$$
dx,dy = r , dr , d\theta
$$
26.3 总结
雅可比矩阵定义:
$$
J = \left[ \frac{\partial f_i}{\partial x_j} \right]
$$雅可比行列式的意义:
- $\det(J) > 0$:变换保持方向。
- $\det(J) < 0$:变换翻转方向。
- $\det(J) = 0$:变换不可逆。
雅可比行列式的应用:
- 积分变换:极坐标、球坐标等。
- 隐函数定理:判断方程组是否可解。
- 几何分析:研究曲面的局部伸缩。
27. 二元函数的泰勒展开
在数学分析中,泰勒展开(Taylor Expansion)用于用多项式逼近光滑函数。对于二元函数 $f(x, y)$,泰勒展开可以表示它在某一点的局部近似。
设 $f(x, y)$ 在点 $(a, b)$ 处具有足够高阶的连续偏导数,则它的 二阶泰勒展开式 为:
$$
f(x, y) \approx f(a, b) + f_x (a, b) (x - a) + f_y (a, b) (y - b)
$$
$$
+\frac{1}{2} \left[ f_{xx} (a, b) (x - a)^2 + 2 f_{xy} (a, b) (x - a)(y - b) + f_{yy} (a, b) (y - b)^2 \right]
$$
其中:
- $f_x = \frac{\partial f}{\partial x}$,$f_y = \frac{\partial f}{\partial y}$ 表示一阶偏导数;
- $f_{xx} = \frac{\partial^2 f}{\partial x^2}$,$f_{yy} = \frac{\partial^2 f}{\partial y^2}$,$f_{xy} = \frac{\partial^2 f}{\partial x \partial y}$ 表示二阶偏导数。
更一般地,n 阶泰勒展开可以写成:
$$
T_n(x, y) = \sum_{i+j \leq n} \frac{1}{i!j!} \frac{\partial^{i+j} f}{\partial x^i \partial y^j} (a, b) (x - a)^i (y - b)^j
$$
其中求和范围是 $i + j \leq n$,即所有偏导数阶数之和不超过 $n$。
27.2 几何意义
- 一阶展开 仅包含线性项,对应于函数在 $(a,b)$ 处的切平面。
- 二阶展开 包含二次项,可以更准确地逼近函数,对应于二次曲面。
- 高阶展开 可以更精确地近似 $f(x, y)$,但计算复杂度更高。
应用
- 函数近似:用低阶多项式代替复杂函数,简化计算。
- 优化问题:二阶泰勒展开用于分析临界点,判断极值(如 Hessian 矩阵)。
- 物理建模:在流体力学、量子力学等领域,用于研究微小扰动。
27.3. 示例
设函数:
$$
f(x, y) = e^x \cos y
$$
在点 $(0,0)$ 处的二阶泰勒展开:
- 计算函数值:
$$
f(0,0) = e^0 \cos 0 = 1
$$ - 计算一阶偏导数:
$$
f_x = e^x \cos y, \quad f_x(0,0) = 1
$$
$$
f_y = -e^x \sin y, \quad f_y(0,0) = 0
$$ - 计算二阶偏导数:
$$
f_{xx} = e^x \cos y, \quad f_{xx}(0,0) = 1
$$
$$
f_{yy} = -e^x \cos y, \quad f_{yy}(0,0) = -1
$$
$$
f_{xy} = -e^x \sin y, \quad f_{xy}(0,0) = 0
$$ - 代入二阶泰勒公式:
$$
f(x, y) \approx 1 + x + \frac{1}{2} (x^2 - y^2)
$$
27.4. 总结
- 一阶泰勒展开:
$$
f(x, y) \approx f(a, b) + f_x (a, b) (x - a) + f_y (a, b) (y - b)
$$ - 二阶泰勒展开:
$$
f(x, y) \approx f(a, b) + f_x (a, b) (x - a) + f_y (a, b) (y - b)
$$
$$
+\frac{1}{2} \left[ f_{xx} (a, b) (x - a)^2 + 2 f_{xy} (a, b) (x - a)(y - b) + f_{yy} (a, b) (y - b)^2 \right]
$$ - 应用:
- 函数近似
- 极值判断
- 物理建模
28. 计算曲线长度
在微积分中,曲线的长度(弧长)可以通过积分计算。我们通常使用参数方程或极坐标方程来描述曲线,并根据不同的表达方式推导相应的弧长公式。
28.1. 采用参数方程的曲线长度
若曲线由参数方程:
$$
x = x(t), \quad y = y(t), \quad t \in [a, b]
$$
给出,则其弧长 $L$ 由以下积分计算:
$$
L = \int_a^b \sqrt{\left( \frac{dx}{dt} \right)^2 + \left( \frac{dy}{dt} \right)^2} , dt
$$
其中:
- $\frac{dx}{dt}$ 和 $\frac{dy}{dt}$ 分别是 $x$ 和 $y$ 对 $t$ 的导数。
- 积分的上限和下限 $a, b$ 是参数 $t$ 的取值范围。
示例
计算圆的四分之一弧长,参数方程:
$$
x = r\cos t, \quad y = r\sin t, \quad t \in [0, \frac{\pi}{2}]
$$
计算导数:
$$
\frac{dx}{dt} = -r\sin t, \quad \frac{dy}{dt} = r\cos t
$$
代入公式:
$$
L = \int_0^{\frac{\pi}{2}} \sqrt{(-r\sin t)^2 + (r\cos t)^2} , dt
$$
$$
= \int_0^{\frac{\pi}{2}} \sqrt{r^2 (\sin^2 t + \cos^2 t)} , dt
$$
$$
= \int_0^{\frac{\pi}{2}} r , dt = r \frac{\pi}{2}
$$
因此,圆的四分之一弧长为:
$$
\frac{\pi r}{2}
$$
28.2. 采用极坐标方程的曲线长度
若曲线由极坐标方程:
$$
r = f(\theta), \quad \theta \in [\alpha, \beta]
$$
给出,则其弧长 $L$ 由以下积分计算:
$$
L = \int_\alpha^\beta \sqrt{ \left( \frac{dr}{d\theta} \right)^2 + r^2 } , d\theta
$$
其中:
- $r = f(\theta)$ 是极坐标曲线的方程。
- $\frac{dr}{d\theta}$ 是 $r$ 对 $\theta$ 的导数。
示例
计算螺旋线 $r = a\theta$ 在 $\theta \in [0, 2\pi]$ 上的弧长:
- 计算导数:
$$
\frac{dr}{d\theta} = a
$$ - 代入弧长公式:
$$
L = \int_0^{2\pi} \sqrt{ a^2 + (a\theta)^2 } , d\theta
$$
$$
= \int_0^{2\pi} \sqrt{ a^2(1 + \theta^2) } , d\theta
$$
该积分一般需要数值方法计算。
28.3. 总结
参数方程的弧长公式:
$$
L = \int_a^b \sqrt{\left( \frac{dx}{dt} \right)^2 + \left( \frac{dy}{dt} \right)^2} , dt
$$- 适用于参数化曲线。
- 计算需要求 $x$ 和 $y$ 对参数 $t$ 的导数。
极坐标方程的弧长公式:
$$
L = \int_\alpha^\beta \sqrt{ \left( \frac{dr}{d\theta} \right)^2 + r^2 } , d\theta
$$- 适用于极坐标曲线。
- 计算需要求 $r$ 对 $\theta$ 的导数。
应用:
- 计算螺旋线、圆弧、摆线等曲线的长度。
- 物理应用:如卫星轨道、波长计算等。
29. 计算平面面积
在微积分中,平面区域的面积可以通过积分计算。根据曲线的表达方式,我们可以使用参数方程或极坐标方程来推导面积公式。
29.1. 采用参数方程计算面积
若区域由参数方程:
$$
x = x(t), \quad y = y(t), \quad t \in [a, b]
$$
给出,我们可以利用格林公式计算面积:
$$
A = \int_a^b x(t) \frac{dy}{dt} , dt
$$
或者:
$$
A = -\int_a^b y(t) \frac{dx}{dt} , dt
$$
其中:
- $\frac{dx}{dt}$ 和 $\frac{dy}{dt}$ 是 $x$ 和 $y$ 对 $t$ 的导数。
示例
求椭圆 $\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$ 的面积,参数方程:
$$
x = a\cos t, \quad y = b\sin t, \quad t \in [0, 2\pi]
$$
计算导数:
$$
\frac{dy}{dt} = b\cos t
$$
代入面积公式:
$$
A = \int_0^{2\pi} a\cos t \cdot b\cos t , dt
$$
$$
= ab \int_0^{2\pi} \cos^2 t , dt
$$
利用 $\int_0^{2\pi} \cos^2 t , dt = \pi$,得:
$$
A = ab\pi
$$
这与椭圆面积公式 $A = \pi ab$ 一致。
29.2. 采用极坐标方程计算面积
若区域由极坐标方程:
$$
r = f(\theta), \quad \theta \in [\alpha, \beta]
$$
给出,则面积 $A$ 由以下积分计算:
$$
A = \frac{1}{2} \int_\alpha^\beta r^2 , d\theta
$$
其中:
- $r = f(\theta)$ 是极坐标曲线的方程。
示例
求极坐标方程 $r = a\cos\theta$ 代表的心形曲线的面积:
- 取对称区域 $0 \leq \theta \leq \pi/2$ 计算面积:
$$
A = \frac{1}{2} \int_0^{\frac{\pi}{2}} (a\cos\theta)^2 , d\theta
$$ - 计算积分:
$$
A = \frac{a^2}{2} \int_0^{\frac{\pi}{2}} \cos^2\theta , d\theta
$$
利用 $\int \cos^2 \theta , d\theta = \frac{\theta}{2} + \frac{\sin 2\theta}{4}$,计算:
$$
A = \frac{a^2}{2} \left( \frac{\pi}{4} + 0 \right) = \frac{a^2\pi}{8}
$$ - 由于曲线关于 $x$ 轴对称,完整的面积为:
$$
A_{\text{总}} = 4 \times \frac{a^2\pi}{8} = \frac{a^2\pi}{2}
$$
29.3. 总结
参数方程的面积公式:
$$
A = \int_a^b x(t) \frac{dy}{dt} , dt
$$
或
$$
A = -\int_a^b y(t) \frac{dx}{dt} , dt
$$- 适用于参数化曲线围成的区域。
- 计算时需要求 $x$ 和 $y$ 对 $t$ 的导数。
极坐标方程的面积公式:
$$
A = \frac{1}{2} \int_\alpha^\beta r^2 , d\theta
$$- 适用于极坐标描述的封闭曲线。
- 计算时需要对 $r^2$ 进行积分。
应用:
- 计算椭圆、心形曲线、玫瑰曲线等的面积。
- 物理应用:如天文学中的行星轨道面积计算等。
30. 圆锥曲线
设圆锥曲线的一般方程为:
$$
Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0
$$
将 $f(x, y)$ 写为上面圆锥曲线的一般式,可以求偏导:
- $\frac{\partial f}{\partial x} = 2Ax + By + D$
- $\frac{\partial f}{\partial y} = 2Cy + Bx + E$
于是,代入点 $(x_0, y_0)$,切线方程为:
$$
(2Ax_0 + By_0 + D)(x - x_0) + (2Cy_0 + Bx_0 + E)(y - y_0) = 0
$$
30.1 椭圆的切线
求椭圆 $\displaystyle \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$ 在点 $(x_0, y_0)$ 处的切线。
将椭圆方程改写为标准形式:
$$
f(x, y) = \frac{x^2}{a^2} + \frac{y^2}{b^2} - 1 = 0
$$
对 $x$、$y$ 分别求偏导:
- $\frac{\partial f}{\partial x} = \frac{2x}{a^2}$
- $\frac{\partial f}{\partial y} = \frac{2y}{b^2}$
代入点 $(x_0, y_0)$,切线方程为:
$$
\frac{2x_0}{a^2}(x - x_0) + \frac{2y_0}{b^2}(y - y_0) = 0
$$
整理得:
$$
\frac{x_0x}{a^2} + \frac{y_0y}{b^2} = 1
$$
这就是椭圆在点 $(x_0, y_0)$ 处的切线方程。
30.2 抛物线的切线公式
设标准抛物线为:
$$
y^2 = 2px
$$
将其写为隐函数形式:
$$
f(x, y) = y^2 - 2px = 0
$$
求偏导数:
- $\frac{\partial f}{\partial x} = -2p$
- $\frac{\partial f}{\partial y} = 2y$
根据切线公式代入得:
$$
(-2p)(x - x_0) + 2y_0(y - y_0) = 0
$$
整理得:
$$
y_0 y = p(x + x_0)
$$
这就是抛物线 $y^2 = 2px$ 在点 $(x_0, y_0)$ 的切线方程。
30.3 双曲线的切线公式
设标准双曲线为:
$$
\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1
$$
写为隐函数形式:
$$
f(x, y) = \frac{x^2}{a^2} - \frac{y^2}{b^2} - 1 = 0
$$
求偏导:
- $\frac{\partial f}{\partial x} = \frac{2x}{a^2}$
- $\frac{\partial f}{\partial y} = -\frac{2y}{b^2}$
代入切线公式:
$$
\frac{2x_0}{a^2}(x - x_0) - \frac{2y_0}{b^2}(y - y_0) = 0
$$
整理得:
$$
\frac{x_0 x}{a^2} - \frac{y_0 y}{b^2} = 1
$$
这就是双曲线 $\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1$ 在点 $(x_0, y_0)$ 的切线方程。
31. 定积分求导
设函数 $f(x, t)$ 关于 $t$ 可积,且在 $x$ 上也具有适当的可导性质。考虑以下形式的积分函数:
$$
F(x) = \int_{a}^{b} f(x, t) , dt
$$
31.1 常数上下限的定积分求导(换序法则)
若 $f(x, t)$ 在 $x$ 关于导数存在,且在 $[a, b]$ 关于 $t$ 连续,则:
$$
\frac{d}{dx} \left( \int_a^b f(x, t) , dt \right) = \int_a^b \frac{\partial f}{\partial x}(x, t) , dt
$$
✅ 这称为「在积分号内求导」的法则。
示例 1
计算:
$$
\frac{d}{dx} \left( \int_0^1 x t^2 , dt \right)
$$
我们有:
$$
f(x, t) = x t^2 \quad \Rightarrow \quad \frac{\partial f}{\partial x} = t^2
$$
所以:
$$
\frac{d}{dx} \left( \int_0^1 x t^2 , dt \right) = \int_0^1 t^2 , dt = \frac{1}{3}
$$
31.2 变上限积分函数的导数(基本形式)
设:
$$
F(x) = \int_a^x f(t) , dt
$$
若 $f(t)$ 在 $[a, x]$ 上连续,则:
$$
\frac{dF}{dx} = f(x)
$$
✅ 这就是著名的「微积分基本定理」的一个形式。
示例 2
设:
$$
F(x) = \int_1^x \ln t , dt
$$
则:
$$
F’(x) = \ln x
$$
31.3 上下限都为函数的情形(莱布尼茨公式)
若:
$$
F(x) = \int_{u(x)}^{v(x)} f(x, t) , dt
$$
则导数为:
$$
F’(x) = f(x, v(x)) \cdot v’(x) - f(x, u(x)) \cdot u’(x) + \int_{u(x)}^{v(x)} \frac{\partial f}{\partial x}(x, t) , dt
$$
✅ 这是最一般形式的定积分求导公式(莱布尼茨公式)。
示例 3
设:
$$
F(x) = \int_{x}^{x^2} \sin t , dt
$$
此时:
- $u(x) = x \Rightarrow u’(x) = 1$
- $v(x) = x^2 \Rightarrow v’(x) = 2x$
- $f(t) = \sin t$
代入公式得:
$$
F’(x) = \sin(x^2) \cdot 2x - \sin(x) \cdot 1 = 2x\sin(x^2) - \sin x
$$
32. 常见三角函数的积、商、幂的积分整理表
三角代换在处理以下三类无理根号表达式的定积分中非常有效:
一、遇到 $\sqrt{a^2 - x^2}$ 类型
令 $x = a\sin\theta$,$\theta \in \left[-\frac{\pi}{2}, \frac{\pi}{2}\right]$
代换后:
$$
\sqrt{a^2 - x^2} = \sqrt{a^2 - a^2\sin^2\theta} = a\cos\theta
$$
示例 1
计算:
$$
\int_0^a \sqrt{a^2 - x^2} , dx
$$
令 $x = a\sin\theta$,则 $dx = a\cos\theta, d\theta$
当 $x = 0 \Rightarrow \theta = 0$,$x = a \Rightarrow \theta = \frac{\pi}{2}$
积分变为:
$$
\int_0^{\pi/2} a\cos\theta \cdot a\cos\theta , d\theta = a^2 \int_0^{\pi/2} \cos^2 \theta , d\theta
= a^2 \cdot \frac{\pi}{4}
$$
所以:
$$
\int_0^a \sqrt{a^2 - x^2} , dx = \frac{\pi a^2}{4}
$$
这实际上是四分之一圆的面积!
二、遇到 $\sqrt{a^2 + x^2}$ 类型
令 $x = a\tan\theta$,$\theta \in \left(-\frac{\pi}{2}, \frac{\pi}{2}\right)$
代换后:
$$
\sqrt{a^2 + x^2} = a\sec\theta
$$
三、遇到 $\sqrt{x^2 - a^2}$ 类型
令 $x = a\sec\theta$,$\theta \in [0, \frac{\pi}{2}) \cup (\pi, \frac{3\pi}{2})$
代换后:
$$
\sqrt{x^2 - a^2} = a\tan\theta
$$
小结图表:三角代换记忆表
| 根号类型 | 代换方法 | $\sqrt{\cdots}$ 的结果 |
|---|---|---|
| $\sqrt{a^2 - x^2}$ | $x = a\sin\theta$ | $a\cos\theta$ |
| $\sqrt{a^2 + x^2}$ | $x = a\tan\theta$ | $a\sec\theta$ |
| $\sqrt{x^2 - a^2}$ | $x = a\sec\theta$ | $a\tan\theta$ |
偷偷说
基本上能把考试要用到的最重要的点Cover掉了;当然求旋转体的体积也是一个很重要的考点,不过偷偷在这里就不赘述了…做数学题这件事仿佛离我的生活越来越远了,但是偷偷一直在用数学的方式在思考:)